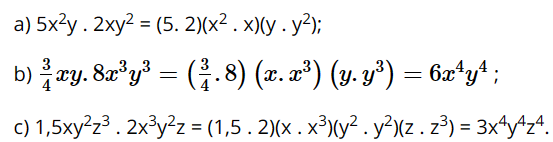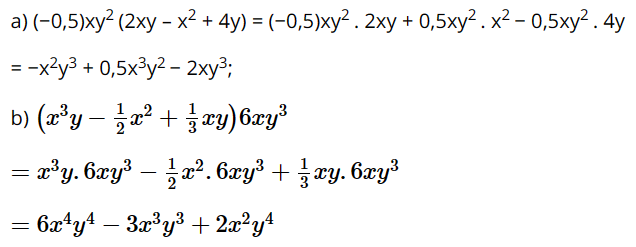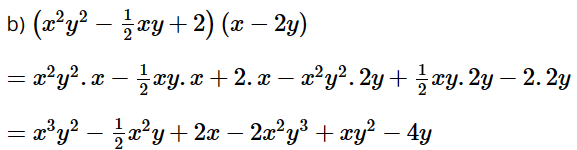Giải SGK Toán 8 trang 21 Kết nối tri thức tập 1

Bài 1.24 trang 21 SGK Toán 8 tập 1 - Kết nối tri thức

Nhân hai đơn thức:

a)      \(5{x^2}y\) và \(2x{y^2}\);

b)      \(\dfrac{3}{4}xy\) và \(8{x^3}{y^2}\);

c)      \(1,5x{y^2}{z^3}\) và \(2{x^3}{y^2}z\).

Phương pháp:

Nối hai đơn thức với nhau bởi dấu nhân rồi bỏ dấu ngoặc (nếu có) và thu gọn đơn thức nhận được.

Lời giải:

Bài 1.25 trang 21 SGK Toán 8 tập 1 - Kết nối tri thức

Tìm tích của đơn thức với đa thức:

a)      \(\left( { - 0,5} \right)x{y^2}\left( {2xy - {x^2} + 4y} \right)\)

b)      \(\left( {{x^3}y - \dfrac{1}{2}{x^2} + \dfrac{1}{3}xy} \right)6x{y^3}\)

Phương pháp:

Muốn nhân đơn thức với đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau. Sau đó, nhóm các hạng tử đồng dạng để thu gọn đa thức.

Lời giải:

Bài 1.26 trang 21 SGK Toán 8 tập 1 - Kết nối tri thức

Rút gọn biểu thức: \(x\left( {{x^2} - y} \right) - {x^2}\left( {x + y} \right) + xy\left( {x - 1} \right)\).

Phương pháp:

Muốn nhân đơn thức với đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau. Sau đó, nhóm các hạng tử đồng dạng để thu gọn đa thức.

Lời giải:

Ta có x(x² – y) – x²(x + y) + xy(x – 1)

= x . x² – x . y – x² . x – x² . y + xy . x – xy . 1

= x³ – xy – x³ – x²y + x²y – xy

= (x³ – x³) + (x²y – x²y) – (xy + xy) = –2xy.

Bài 1.27 trang 21 SGK Toán 8 tập 1 - Kết nối tri thức

Làm tính nhân:

a)      \(\left( {{x^2} - xy + 1} \right)\left( {xy + 3} \right)\)

b)      \(\left( {{x^2}{y^2} - \dfrac{1}{2}xy + 2} \right)\left( {x - 2y} \right)\)

Phương pháp:

Muốn nhân hai đa thức ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các kết quả với nhau.

Lời giải:

a) (x² – xy + 1)(xy + 3)

= x² . xy – xy . xy + 1 . xy + x² . 3 – xy . 3 + 1 . 3

= x³y – x²y² + xy + 3x² – 3xy + 3

= x³y – x²y² + (xy – 3xy) + 3x² + 3

= x³y – x²y² – 2xy + 3x² + 3.

Bài 1.28 trang 21 SGK Toán 8 tập 1 - Kết nối tri thức

Rút gọn biểu thức sau để thấy rằng giá trị của nó không phụ thuộc vào giá trị của biến: \(\left( {x - 5} \right)\left( {2x + 3} \right) - 2x\left( {x - 3} \right) + x + 7\).

Lời giải:

\(\begin{array}{l}\left( {x - 5} \right)\left( {2x + 3} \right) - 2x\left( {x - 3} \right) + x + 7\\ = x.2x + x.3 - 5.2x - 5.3 - 2x.x + 2x.3 + x + 7\\ = 2{x^2} + 3x - 10x - 15 - 2{x^2} + 6x + x + 7\\ = \left( {2{x^2} - 2{x^2}} \right) + \left( {3x - 10x + 6x + x} \right) + \left( { - 15 + 7} \right)\\ =  - 8\end{array}\)

Do đó, giá trị cỉa biểu thức không phụ thuộc vào giá trị của biến.

Bài 1.29 trang 21 SGK Toán 8 tập 1 - Kết nối tri thức

Chứng minh đẳng thức sau: \(\left( {2x + y} \right)\left( {2{x^2} + xy - {y^2}} \right) = \left( {2x - y} \right)\left( {2{x^2} + 3xy + {y^2}} \right)\).

Phương pháp:

Thực hiện phép nhân đa thức với đa thức ở 2 vế.

Muốn nhân đơn thức với đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau. Sau đó, nhóm các hạng tử đồng dạng để thu gọn đa thức.

Lời giải:

Ta có:

• (2x + y)(2x² + xy – y²)

= 2x . 2x² + 2x . xy – 2x . y² + y . 2x² + y . xy – y . y²

= 4x³ + 2x²y – 2xy² + 2x²y + xy² – y³

= 4x³ + (2x²y + 2x²y) + (xy² – 2xy²) – y³

= 4x³ + 4x²y – xy² – y³.

• (2x – y)(2x² + 3xy + y²)

= 2x . 2x² + 2x . 3xy + 2x . y² – y . 2x² – y . 3xy – y . y²

= 4x³ + 6x²y + 2xy² – 2x²y – 3xy² – y³

= 4x³ + (6x²y – 2x²y) + (2xy² – 3xy²) – y³

= 4x³ + 4x²y – xy² – y³.

Do đó (2x + y)(2x² + xy – y²) = (2x – y)(2x² + 3xy + y²) = 4x³ + 4x²y – xy² – y³.

Vậy (2x + y)(2x² + xy – y²) = (2x – y)(2x² + 3xy + y²).

Sachbaitap.com