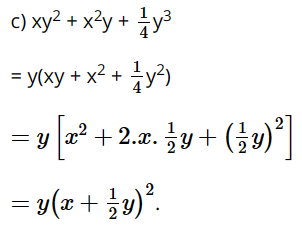Giải SGK Toán 8 trang 25 Chân trời sáng tạo tập 1

Bài 1 trang 25 SGK Toán 8 tập 1 - Chân trời sáng tạo

Phân tích các đa thức sau thành nhân tử:

a) \({x^3} + 4x\)

b) \(6ab - 9a{b^2}\)

c) \(2a\left( {x - 1} \right) + 3b\left( {1 - x} \right)\)

d) \({\left( {x - y} \right)^2} - x\left( {y - x} \right)\)

Phương pháp:

Phân tích đa thức thành nhân tử bằng cách nhóm nhân tử chung

Lời giải:

a) x³ + 4x = x.x² + x.4 = x(x² + 4).

b) 6ab – 9ab² = 3ab.2 – 3ab.3b = 3ab(2 – 3b).

c) 2a(x – 1) + 3b(1 – x)

= 2a(x – 1) + 3b[– (x – 1)]

= 2a(x – 1) – 3b(x – 1)

= (x – 1)(2a – 3b).

d) (x – y)² – x(y – x)

= (x – y)² + x(x – y)

= (x – y)(x – y + x)

= (x – y)(2x – y).

Bài 2 trang 25 SGK Toán 8 tập 1 - Chân trời sáng tạo

Phân tích các đa thức sau thành nhân tử:

a) \(4{x^2} - 1\)

b) \({\left( {x + 2} \right)^2} - 9\)

c) \({\left( {a + b} \right)^2} - {\left( {a - 2b} \right)^2}\)

Phương pháp:

Phân tích đa thức bằng cách sử dụng hằng đẳng thức đáng nhớ

Lời giải:

a) 4x² – 1 = (2x)² – 1² = (2x + 1)(2x –1).

b) (x + 2)² – 9 = (x + 2)² – 3²

                       = (x + 2 + 3)(x + 2 – 3)

                       = (x + 5)(x – 1).

c) (a + b)² – (a – 2b)²

= [(a + b) + (a – 2b)] . [(a + b) – (a – 2b)]

= [a + b + a – 2b] . [a + b – a + 2b]

= (2a – b).3b.

Bài 3 trang 25 SGK Toán 8 tập 1 - Chân trời sáng tạo

Phân tích các đa thức sau thành nhân tử:

a) \(4{a^2} + 4a + 1\)

b) \( - 3{x^2} + 6xy - 3{y^2}\)

c) \({\left( {x + y} \right)^2} - 2\left( {x + y} \right)z + {z^2}\)

Phương pháp:

Phân tích đa thức thành nhân tử bằng cách sử dụng hằng đẳng thức đáng nhớ

Lời giải:

a) 4a² + 4a + 1

= (2a)² + 2.2a.1 + 1²

= (2a + 1)².

b) –3x² + 6xy – 3y²

= –3(x² – 2xy + y²)

= –3(x – y)².

c) (x + y)² – 2(x + y)z + z²

= [(x + y) – z]²

= (x + y – z)².

Bài 4 trang 25 SGK Toán 8 tập 1 - Chân trời sáng tạo

Phân tích các đa thức sau thành nhân tử:

a) \(8{x^3} - 1\)

b) \({x^3} + 27{y^3}\)

c) \({x^3} - {y^6}\)

Phương pháp:

Phân tích đa thức thành nhân tử bằng cách sử dụng hằng đẳng thức đáng nhớ

Lời giải:

a) 8x³ – 1

= (2x)³ – 1³

= (2x – 1)[(2x)² + 2x.1 + 1²]

= (2x – 1)(4x² + 2x + 1).

b) x³ + 27y³

= x³ + (3y)³

= (x + 3y)[x² – x.3y + (3y)²]

= (x + 3y)(x² – 3xy + 9y²).

c) x³ – y⁶

= x³ – (y²)³

= (x – y²)[x² + x.y² + (y²)²]

= (x – y²)(x² + xy² + y⁴).

Bài 5 trang 25 SGK Toán 8 tập 1 - Chân trời sáng tạo

Phân tích các đa thức sau thành nhân tử:

a) \(4{x^3} - 16x\)

b) \({x^4} - {y^4}\)

c) \(x{y^2} + {x^2}y + \dfrac{1}{4}{y^3}\)

d) \({x^2} + 2x - {y^2} + 1\)

Phương pháp:

Phân tích đa thức thành nhân tử bằng cách nhóm nhân tử chung và sử dụng hằng đẳng thức đáng nhớ

Lời giải:

a) 4x³ – 16x

= 4x(x² – 4)

= 4x(x² – 2²)

= 4x(x + 2)(x – 2).

b) x⁴ – y⁴

= (x²)² – (y²)²

= (x² + y²)(x² – y²)

= (x² + y²)(x + y)(x – y).

Bài 6 trang 25 SGK Toán 8 tập 1 - Chân trời sáng tạo

Phân tích các đa thức sau thành nhân tử:

a) \({x^2} - xy + x - y\)

b) \({x^2} + 2xy - 4x - 8y\)

c) \({x^3} - {x^2} - x + 1\)

Phương pháp:

Phân tích đa thức thành nhân tử bằng cách nhóm nhâna tử chung

Lời giải:

a) x² – xy + x – y

= (x² – xy) + (x – y)

= x(x – y) + (x – y)

= (x – y)(x + 1).

b) x² + 2xy – 4x – 8y

= (x² + 2xy) – (4x + 8y)

= x(x +  2y) – 4(x + 2y)

= (x +  2y)(x – 4).

c) x³ – x² – x + 1

= (x³ – x²) – (x – 1)

= x²(x – 1) – (x – 1)

= (x – 1)(x² – 1)

= (x – 1)(x + 1)(x – 1)

= (x – 1)²(x + 1).

Bài 7 trang 25 SGK Toán 8 tập 1 - Chân trời sáng tạo

Cho \(y > 0\). Tìm độ dài cạnh của hình vuông có diện tích bằng \(49{y^2} + 28y + 4\)

Phương pháp:

Sử dụng những hằng đẳng thức đáng nhớ để tìm cạnh hình vuông

Lời giải:

Giả sử hình vuông có độ dài cạnh bằng a (a > 0), khi đó diện tích của hình vuông là a².

Tức là 49y² + 28y + 4 = a².

Ta phân tích đa thức 49y² + 28y + 4 thành nhân tử có dạng a².

49y² + 28y + 4

= (7y)² + 2.7y.2 + 2²

= (7y + 2)²

Vậy độ dài cạnh của hình vuông có diện tích bằng 49y² + 28y + 4 là 7y + 2.

 Sachbaitap.com