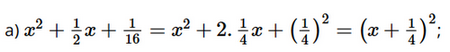Giải SGK Toán 8 trang 28 Cánh Diều tập 1Giải bài 1, 2, 3, 4, 5, 6 trang 28 trang 28 SGK Toán lớp 8 Cánh Diều tập 1. Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến: Bài 1 trang 28 SGK Toán 8 tập 1 - Cánh Diều Cho hai đa thức: \(A = 4{{\rm{x}}^6} - 2{{\rm{x}}^2}{y^3} - 5{\rm{x}}y + 2;\mathop {}\limits^{} B = 3{{\rm{x}}^2}{y^3} + 5{\rm{x}}y - 7\) a) Tính giá trị của mỗi đa thức A, B tại x = -1; y = 1 b) Tính A + B; A - B Phương pháp: a) Thay các giá trị x, y cho trước vào đa thức A, B để tính giá trị b) Tính A + B, A – B bằng nhóm các đơn thức đồng dạng và rút gọn Lời giải: a) • Giá trị của mỗi đa thức A tại x = –1; y = 1 là: 4 . (–1)6 – 2 . (–1)2 . 13 – 5 . (–1) . 1 + 2 = 4 – 2 + 5 + 2 = 9. • Giá trị của mỗi đa thức B tại x = –1; y = 1 là: 3 . (–1)2 . 13 + 5 . (–1) . 1 – 7 = 3 – 5 – 7 = –9. b) Ta có: • A + B = (4x6 – 2x2y3 – 5xy + 2) + (3x2y3 + 5xy – 7) = 4x6 – 2x2y3 – 5xy + 2 + 3x2y3 + 5xy – 7 = 4x6 + (3x2y3 – 2x2y3) + (5xy – 5xy) + (2 – 7) = 4x6 + x2y3 – 5. • A – B = (4x6 – 2x2y3 – 5xy + 2) – (3x2y3 + 5xy – 7) = 4x6 – 2x2y3 – 5xy + 2 – 3x2y3 – 5xy + 7 = 4x6 – (3x2y3 + 2x2y3) – (5xy + 5xy) + (2 + 7) = 4x6 – 5x2y3 – 10xy + 9. Vậy A + B = 4x6 + x2y3 – 5; A – B = 4x6 – 5x2y3 – 10xy + 9. Bài 2 trang 28 SGK Toán 8 tập 1 - Cánh Diều Thực hiện phép tính: \(a) - \dfrac{1}{3}{a^2}b\left( { - 6{\rm{a}}{b^2} - 3{\rm{a}} + 9{b^3}} \right)\) \(b)\left( {{a^2} + {b^2}} \right)\left( {{a^4} - {a^2}{b^2} + {b^4}} \right)\) \(c)\left( { - 5{{\rm{x}}^3}{y^3}z} \right):\left( {\dfrac{{15}}{2}x{y^2}z} \right)\) \(d)\left( {8{{\rm{x}}^4}{y^2} - 10{{\rm{x}}^2}{y^4} + 12{{\rm{x}}^3}{y^5}} \right):\left( { - 2{{\rm{x}}^2}{y^2}} \right)\) Phương pháp: Áp dụng các quy tắc nhân đơn thức với đa thức, nhân đa thức với đa thức, chia đơn thức cho đơn thức, chia đa thức cho đơn thức đối với đa thức nhiều biên để thực hiện phép tính. Lời giải: \(\begin{array}{l}a) - \dfrac{1}{3}{a^2}b\left( { - 6{\rm{a}}{b^2} - 3{\rm{a}} + 9{b^3}} \right)\\ = \left( { - \dfrac{1}{3}{a^2}b} \right).\left( { - 6{\rm{a}}{b^2}} \right) + \left( { - \dfrac{1}{3}{a^2}b} \right).\left( { - 3{\rm{a}}} \right) + \left( { - \dfrac{1}{3}{a^2}b} \right).\left( {9{b^3}} \right)\\ = 2{{\rm{a}}^3}{b^4} + {a^3}b - 3{\rm{a}}{b^4}\end{array}\) \(b)\left( {{a^2} + {b^2}} \right)\left( {{a^4} - {a^2}{b^2} + {b^4}} \right) = {\left( {{a^2}} \right)^3} + {\left( {{b^2}} \right)^3} = {a^6} + {b^6}\) \(\begin{array}{l}c)\left( { - 5{{\rm{x}}^3}{y^3}z} \right):\left( {\dfrac{{15}}{2}x{y^2}z} \right)\\ = \left( { - 5:\dfrac{{15}}{2}} \right).\left( {{x^3}:x} \right).\left( {{y^3}:{y^2}} \right).\left( {z:z} \right) = \dfrac{{ - 2}}{3}{x^2}\end{array}\) \(\begin{array}{l}d)\left( {8{{\rm{x}}^4}{y^2} - 10{{\rm{x}}^2}{y^4} + 12{{\rm{x}}^3}{y^5}} \right):\left( { - 2{{\rm{x}}^2}{y^2}} \right)\\ = \left[ {\left( {8{{\rm{x}}^4}{y^2}} \right):\left( { - 2{{\rm{x}}^2}{y^2}} \right)} \right] + \left[ {\left( { - 10{x^2}{y^4}} \right):\left( { - 2{{\rm{x}}^2}{y^2}} \right)} \right] + \left[ {\left( {12{{\rm{x}}^3}{y^5}} \right):\left( { - 2{{\rm{x}}^2}{y^2}} \right)} \right]\\ = - 4{{\rm{x}}^2} + 5{y^2} - 6{\rm{x}}{y^3}\end{array}\) Bài 3 trang 28 SGK Toán 8 tập 1 - Cánh Diều Viết mỗi biểu thức sau dưới dạng bình phương, lập phương của một tổng hoặc một hiệu: \(a){x^2} + \dfrac{1}{2}x + \dfrac{1}{{16}}\) \(b)25{{\rm{x}}^2} - 10{\rm{x}}y + {y^2}\) \(c){x^3} + 9{{\rm{x}}^2}y + 27{\rm{x}}{y^2} + 27{y^3}\) \(d)8{{\rm{x}}^3} - 12{{\rm{x}}^2}y + 6{\rm{x}}{y^2} - {y^3}\) Phương pháp: Vận dụng các hằng đẳng thức đã học để viết các biểu thức. Lời giải:
b) 25x2 – 10xy + y2 = (5x)2 – 2 . 5x . y + y2 = (5x – y)2; c) x3 + 9x2y + 27xy2 + 27y3 = x3 + 3 . x2. 3y + 3 . x . (3y)2 + (3y)3 = (x + 3y)3; d) 8x3 – 12x2y + 6xy2 – y3 = (2x)3 – 3 . (2x)2 . y + 3 . 2x . y2 – y3 = (2x – y)3. Bài 4 trang 28 SGK Toán 8 tập 1 - Cánh Diều Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến: a) \(A = 0,2\left( {5{\rm{x}} - 1} \right) - \dfrac{1}{2}\left( {\dfrac{2}{3}x + 4} \right) + \dfrac{2}{3}\left( {3 - x} \right)\) b) \(B = \left( {x - 2y} \right)\left( {{x^2} + 2{\rm{x}}y + 4{y^2}} \right) - \left( {{x^3} - 8{y^3} + 10} \right)\) c) \(C = 4{\left( {x + 1} \right)^2} + {\left( {2{\rm{x}} - 1} \right)^2} - 8\left( {x - 1} \right)\left( {x + 1} \right) - 4{\rm{x}}\) Phương pháp: Áp dụng các quy tắc của phép tính đa thức nhiều biến, các hằng đẳng thức đã học để tính giá trị các biểu thức đã cho mà kết quả không chứa biến. Lời giải: a) \(\begin{array}{l}A = 0,2\left( {5{\rm{x}} - 1} \right) - \dfrac{1}{2}\left( {\dfrac{2}{3}x + 4} \right) + \dfrac{2}{3}\left( {3 - x} \right)\\A = x - 0,2 - \dfrac{1}{3}x - 2 + 2 - \dfrac{2}{3}x\\ = \left( {x - \dfrac{1}{3}x - \dfrac{2}{3}x} \right) + \left( {\dfrac{{ - 1}}{2} - 2 + 2} \right)\\ = - \dfrac{1}{2}\end{array}\) Vậy \(A = - \dfrac{1}{2}\) không phụ thuộc vào biến x b) \(\begin{array}{l}B = \left( {x - 2y} \right)\left( {{x^2} + 2{\rm{x}}y + 4{y^2}} \right) - \left( {{x^3} - 8{y^3} + 10} \right)\\B = \left[ {x - {{\left( {2y} \right)}^3}} \right] - {x^3} - 8{y^3} - 10\\B = {x^3} - 8{y^3} - {x^3} - 8{y^3} - 10 = - 10\end{array}\) Vậy B = -10 không phụ thuộc vào biến x, y. c) \(\begin{array}{l}C = 4{\left( {x + 1} \right)^2} + {\left( {2{\rm{x}} - 1} \right)^2} - 8\left( {x - 1} \right)\left( {x + 1} \right) - 4{\rm{x}}\\{\rm{C = 4}}\left( {{x^2} + 2{\rm{x}} + 1} \right) + \left( {4{{\rm{x}}^2} - 4{\rm{x}} + 1} \right) - 8\left( {{x^2} - 1} \right) - 4{\rm{x}}\\C = 4{{\rm{x}}^2} + 8{\rm{x}} + 4 + 4{{\rm{x}}^2} - 4{\rm{x}} + 1 - 8{{\rm{x}}^2} + 8 - 4{\rm{x}}\\C = \left( {4{{\rm{x}}^2} + 4{{\rm{x}}^2} - 8{{\rm{x}}^2}} \right) + \left( {8{\rm{x}} - 4{\rm{x}} - 4{\rm{x}}} \right) + \left( {4 + 1 + 8} \right)\\C = 13\end{array}\) Vậy C = 13 không phụ thuộc vào biến x Bài 5 trang 28 SGK Toán 8 tập 1 - Cánh Diều Phân tích mỗi đa thức sau thành nhân tử: a) \({\left( {x + 2y} \right)^2} - {\left( {x - y} \right)^2}\) b) \({\left( {x + 1} \right)^3} + {\left( {x - 1} \right)^3}\) c) \(\left( {2y - 3} \right)x + 4y\left( {2y - 3} \right)\) d) \(10{\rm{x}}\left( {x - y} \right) - 15{{\rm{x}}^2}\left( {y - x} \right)\) e) \({x^3} + 3{{\rm{x}}^2} + 3{\rm{x}} + 1 - {y^3}\) g) \({x^3} - 2{{\rm{x}}^2}y + x{y^2} - 4{\rm{x}}\) Phương pháp: Vận dụng trực tiếp hằng đẳng thức hoặc vận dụng hằng đẳng thức để nhóm các hạng tử để phân tích đa thức thành nhân tử. Lời giải: a) \(\begin{array}{l}{\left( {x + 2y} \right)^2} - {\left( {x - y} \right)^2}\\ = \left( {x + 2y + x - y} \right)\left( {x + 2y - x + y} \right)\\ = \left( {2{\rm{x}} + y} \right).3y\end{array}\) b) \(\begin{array}{l}{\left( {x + 1} \right)^3} + {\left( {x - 1} \right)^3}\\ = \left( {x + 1 + x - 1} \right)\left[ {{{\left( {x + 1} \right)}^2} - \left( {x + 1} \right)\left( {x - 1} \right) + {{\left( {x - 1} \right)}^2}} \right]\\ = 2{\rm{x}}\left[ {{x^2} + 2{\rm{x}} + 1 - \left( {{x^2} - 1} \right) + {x^2} - 2{\rm{x}} + 1} \right]\\ = 2{\rm{x}}\left( {{x^2} + 2{\rm{x}} + 1 - {x^2} + 1 + {x^2} - 2{\rm{x}} + 1} \right)\\ = 2{\rm{x}}\left( {{x^2} + 3} \right)\end{array}\) c) \(\left( {2y - 3} \right)x + 4y\left( {2y - 3} \right) = \left( {2y - 3} \right)\left( {1 + 4y} \right)\) d) \(\begin{array}{l}10{\rm{x}}\left( {x - y} \right) - 15{{\rm{x}}^2}\left( {y - x} \right)\\ = 10{\rm{x}}\left( {x - y} \right) + 15{{\rm{x}}^2}\left( {x - y} \right)\\ = \left( {x - y} \right)\left( {10{\rm{x}} + 15{{\rm{x}}^2}} \right)\\ = \left( {x - y} \right).5{\rm{x}}\left( {2 + 3{\rm{x}}} \right)\\ = 5{\rm{x}}\left( {x - y} \right)\left( {2 + 3{\rm{x}}} \right)\end{array}\) e) \(\begin{array}{l}{x^3} + 3{{\rm{x}}^2} + 3{\rm{x}} + 1 - {y^3}\\ = \left( {{x^3} + 3{{\rm{x}}^2} + 3{\rm{x}} + 1} \right) - {y^3}\\ = {\left( {x + 1} \right)^3} - {y^3}\\ = \left( {x + 1 - y} \right)\left[ {{{\left( {x + 1} \right)}^2} + \left( {x + 1} \right)y + {y^2}} \right]\end{array}\) g) \(\begin{array}{l}{x^3} - 2{{\rm{x}}^2}y + x{y^2} - 4{\rm{x}}\\{\rm{ = }}\left( {{x^3} - 2{{\rm{x}}^2}y + x{y^2}} \right) - 4{\rm{x}}\\ = x\left( {{x^2} - 2{\rm{x}}y + {y^2}} \right) - 4{\rm{x}}\\ = x{\left( {x - y} \right)^2} - 4{\rm{x}}\\ = x\left[ {{{\left( {x - y} \right)}^2} - {2^2}} \right]\\ = x\left( {x - y + 2} \right)\left( {x - y - 2} \right)\end{array}\) Bài 6 trang 28 SGK Toán 8 tập 1 - Cánh Diều Một mảnh vườn có dạng hình chữ nhật với chiều rộng là x (m), chiều dài là y (m). a) Viết đa thức biểu thị diện tích của mảnh vườn b) Nếu tăng chiều rộng lên 2m và giảm chiều dài đi 3 m thì được mảnh vườn mới. Viết đa thức biểu thị diện tích của mảnh vườn mới. c) Viết đa thức biểu thị phần diện tích lớn hơn của mảnh vườn mới so với mảnh vườn ban đầu. Phương pháp: Theo công thức tính diện tích hình chữ nhật khi biết chiều rộng và chiều dài để viết biểu thức. Lời giải: a) Đa thức biểu thị diện tích của mảnh vườn hình chữ nhật là xy. b) Chiều rộng mảnh vườn sau khi tăng là: x + 2 (m); Chiều dài mảnh vườn sau khi giảm là: y – 3 (m); Đa thức biểu thị diện tích của mảnh vườn mới là: (x + 2)(y – 3) = xy – 3x + 2y – 6. c) Đa thức biểu thị phần diện tích lớn hơn của mảnh vườn mới so với mảnh vườn ban đầu là: (xy – 3x + 2y – 6) – xy = 2y – 3x – 6. Sachbaitap.com
Xem thêm tại đây:
Bài tập cuối Chương 1
|
-

Giải SGK Toán 8 trang 37 Cánh Diều tập 1
Giải bài 1, 2, 3, 4, 5, 6 trang 37 SGK Toán lớp 8 Cánh Diều tập 1. Quy đồng mẫu thức các phân thức trong mỗi trường hợp sau:

 Tải ngay
Tải ngay