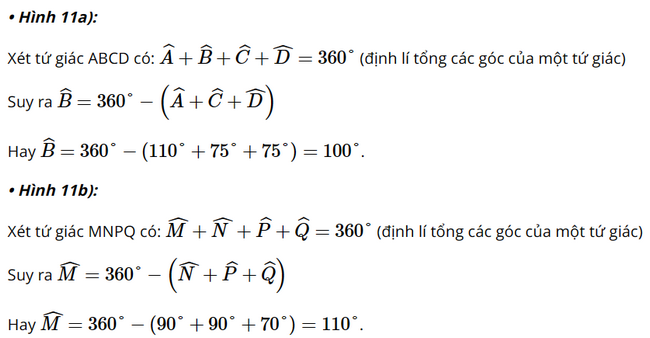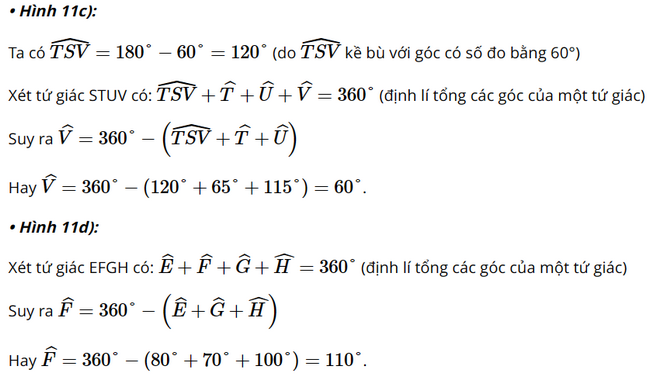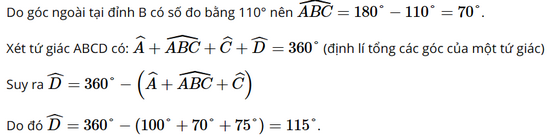Giải SGK Toán 8 trang 66, 67 Chân trời sáng tạo tập 1Giải bài 1, 2 trang 66, bài 3, 4, 5, 6, 7 trang 67 SGK Toán lớp 8 chân trời sáng tạo tập 1. Bài 1. Tìm số đo các góc chưa biết của các tứ giác trong Hình 11. Bài 1 trang 66 SGK Toán 8 tập 1 - Chân trời sáng tạo Tìm số đo các góc chưa biết của các tứ giác trong Hình 11.
Phương pháp: Sử dụng tính chất tổng số đo bốn góc của một tứ giác bằng \(360^\circ \) vào tứ giác \(ABCD\), \(MNPQ\) và \(UTSV\) Lời giải:
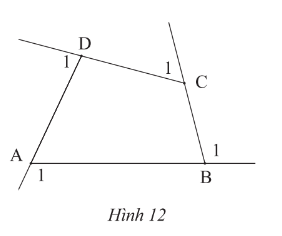
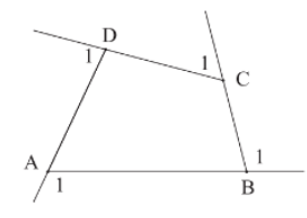
Bài 2 trang 66 SGK Toán 8 tập 1 - Chân trời sáng tạo Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó. Hãy tính tổng số đo bốn góc ngoài \(\widehat {{A_1}};\;\widehat {{B_1}};\;\widehat {{C_1}};\;\widehat {{D_1}}\) của tứ giác \(ABCD\) ở hình 12.
Phương pháp: Sử dụng tính chất tổng các góc trong một tứ giác bằng \(360^\circ \) Lời giải:
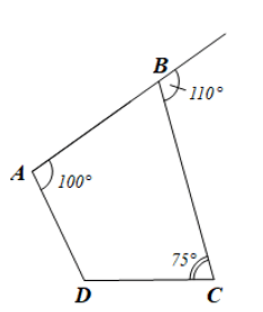
Bài 3 trang 67 SGK Toán 8 tập 1 - Chân trời sáng tạo Tứ giác \(ABCD\) có \(\widehat A = 100^\circ \), góc ngoài tại đỉnh \(B\) bằng \(110^\circ \), \(\widehat C = 75^\circ \). Tính số đo góc \(D\) Phương pháp: Tính số đo góc \(B\) Sử dụng tính chất tổng các góc trong tứ giác bằng \(360^\circ \) để tính số đo góc \(D\) Lời giải:
Bài 4 trang 67 SGK Toán 8 tập 1 - Chân trời sáng tạo Tứ giác \(ABCD\) có góc ngoài tại đỉnh \(A\) bằng \(65^\circ \), góc ngoài tại đỉnh \(B\) bằng \(100^\circ \), góc ngoài tại đỉnh \(C\) bằng \(60^\circ \). Tính số đo góc ngoài tại đỉnh \(D\). Phương pháp: Sử dụng tính chất tổng các góc ngoài của một tứ giác bằng \(360^\circ \) Lời giải:
Bài 5 trang 67 SGK Toán 8 tập 1 - Chân trời sáng tạo Tứ giác \(ABCD\) có số đo \(\widehat A = x;\;\widehat B = 2x;\;\widehat C = 3x;\;\widehat D = 4x\). Tính số đo các góc của tứ giác đó. Phương pháp: Sử dụng tính chất tổng các góc của một tứ giác bằng \(360^\circ \) Tìm \(x\) Tính số đo các góc của tứ giác \(ABCD\) Lời giải:
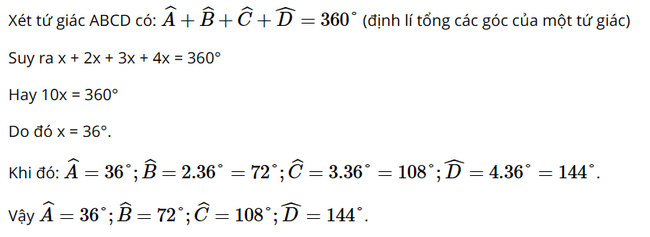 Bài 6 trang 67 SGK Toán 8 tập 1 - Chân trời sáng tạo
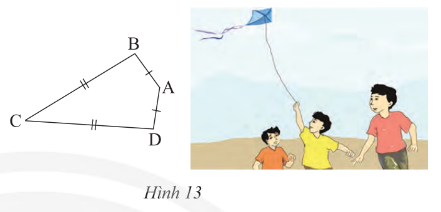
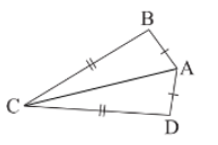
Ta gọi tứ giác ABCD với AB = AD, CB = CD (hình 13) là hình “cái diều”. a. Chứng minh rằng AC là đường trung trực của BD. b. Cho biết \(\widehat B = {95^0},\widehat C = {35^0}.\)Tính \(\widehat A\) và \(\widehat D\)
Phương pháp: a) Sử dụng tính chất của đường trung trực để chứng minh \(AC\) là trung trực của \(BD\) b) Sử dụng tính chất tổng bốn góc trong tứ giác \(ABCD\) Lời giải:
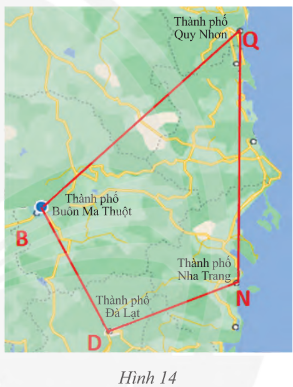
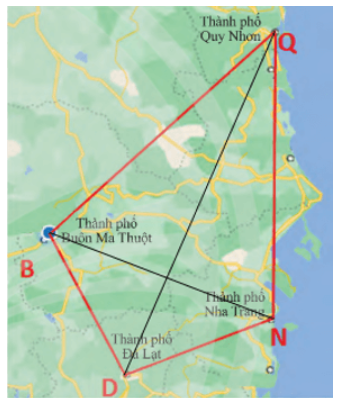
Bài 7 trang 67 SGK Toán 8 tập 1 - Chân trời sáng tạo Trên bản đồ, tứ giác \(BDNQ\) với các đỉnh là các thành phố Buôn Ma Thuột, Đà Lạt, Nha Trang, Quy Nhơn. a) Tìm các cạnh kề và cạnh đối diện của cạnh \(BD\). b) Tìm các đường chéo của tứ giác
Phương pháp: Sử dụng kiến thức về đặc điểm của tứ giác để trả lời các câu hỏi Lời giải:
a) Tứ giác BDNQ có: • Các cạnh kề: BD và BQ; DB và DN; ND và NQ; QN và QB; • Các cạnh đối: BD và NQ; DN và BQ. b) Tứ giác BDNQ có các đường chéo BN và DQ. Sachbaitap.com
Xem thêm tại đây:
Bài 2. Tứ giác
|
-

Giải SGK Toán 8 trang 71, 72 Chân trời sáng tạo tập 1
Giải bài 1, 2 trang 71, bài 3. 4. 5. 6. 7 trang 72 SGK Toán lớp 8 chân trời sáng tạo tập 1. Bài 2. Cho tứ giác ABCD có AB = AD, BD là tia phân giác của góc B. Chứng minh rằng ABCD là hình thang.

 Tải ngay
Tải ngay