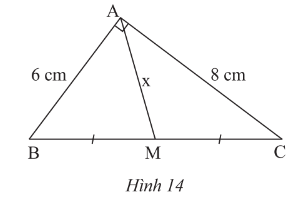
Giải SGK Toán 8 trang 87 Chân trời sáng tạo tập 1

Bài 1 trang 87 SGK Toán 8 tập 1 - Chân trời sáng tạo

Cho Hình 14. Tìm \(x\).

Phương pháp:

Áp dụng ĐL Pythagore vào tam giác vuông \(ABC\) 

Lời giải:

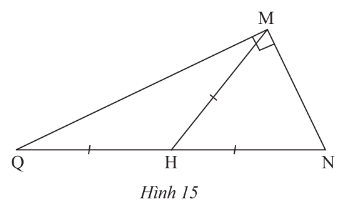
Bài 2 trang 87 SGK Toán 8 tập 1 - Chân trời sáng tạo

Cho Hình 15. Vẽ thêm điểm \(P\) để tứ giác \(MNPQ\) là hình chữ nhật

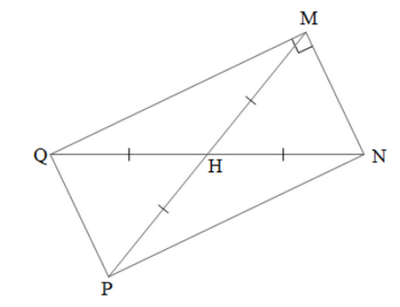
Phương pháp:

Vẽ \(MP = NQ\) (ba điểm \(M,H,P\) thẳng hàng)

Khi đó ta được hình chữ nhật \(MNPQ\)

Lời giải:

Lấy điểm P sao cho H là trung điểm của MP (hình vẽ).

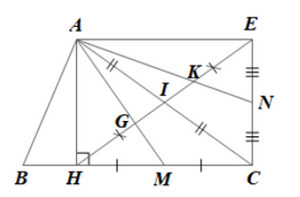
Bài 3 trang 87 SGK Toán 8 tập 1 - Chân trời sáng tạo

Cho tam giác \(ABC\) có đường cao \(AH\). Gọi \(I\) là trung điểm của \(AC\), \(E\) là điểm đối xứng với \(H\) qua \(I\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(HC\), \(CE\). Các đường thẳng \(AM\), \(AN\) cắt \(HE\) tại \(G\) và \(K\).

a) Chứng minh tứ giác \(AHCE\) là hình chữ nhật

b) Chứng minh \(HG = GK = KE\) 

Phương pháp:

a) Áp dụng các dấu hiệu nhận biết của hình chữ nhật

b) Áp dụng tính chất trọng tâm của tam giác

Lời giải:

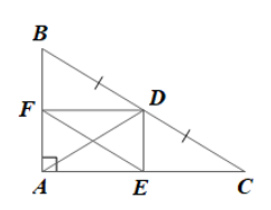
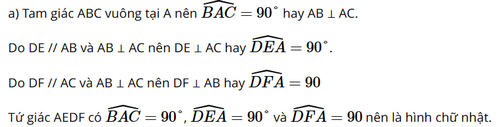
Bài 4 trang 87 SGK Toán 8 tập 1 - Chân trời sáng tạo

Cho tam giác \(ABC\) vuông tại \(A\) (\(AB < AC\). Gọi \(D\) là trung điểm của \(BC\). Vẽ \(DE\) // \(AB\), vẽ \(DF\) // \(AC\) \((E \in AC\); \(F \in AB)\). Chứng minh rằng:

a) Tứ giác \(AEDF\) là hình chữ nhật

b) Tứ giác \(BFED\) là hình bình hành

Phương pháp:

a) Áp dụng dấu hiệu nhận biết hình chữ nhật

b) Áp dụng dấu hiệu nhận biết hình bình hành

Lời giải:

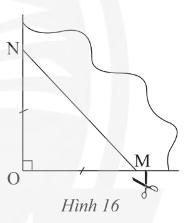
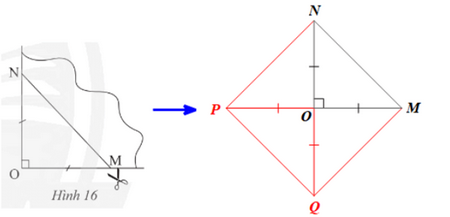
Bài 5 trang 87 SGK Toán 8 tập 1 - Chân trời sáng tạo

Lấy một tờ giấy, gấp làm tư để có một góc vuông như triong Hình 16, dùng kéo cắt theo đường \(MN\) sao cho \(OM = ON\). Mở phần giấy cắt được ra ta được một tứ giác. Tứ giác đó là hình gì. Giải thích kết luận của em.

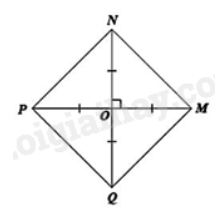
Phương pháp:

Mở tờ giấy được cắt ra ta được tứ giác \(MNPQ\) như hình vẽ dưới đây

Áp dụng dấu hiệu nhận biết hình vuông để chứng minh tức giác \(MNPQ\) là hình vuông

Lời giải:

Mở phần giấy cắt được ra ta được một tứ giác MNPQ như hình vẽ trên.

Ta có OM = ON = OP = OQ nên:

• O là trung điểm của MP và NQ;

• MP = OM + OP = 2OM và NQ = ON + OQ = 2ON

Suy ra MP = NQ.

Xét tứ giác MNPQ có hai đường chéo MP và NQ cắt nhau tại trung điểm O của mỗi đường nên là hình bình hành.

Lại có hai đường chéo bằng nhau MP = NQ nên là hình chữ nhật.

Mặt khác MP ⊥ NQ nên hình chữ nhật MNPQ có hai đường chéo vuông góc với nhau.

Do đó MNPQ là hình vuông.

Sachbaitap.com