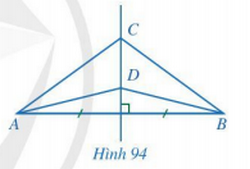
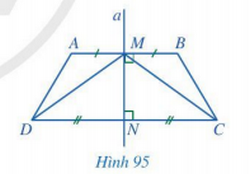
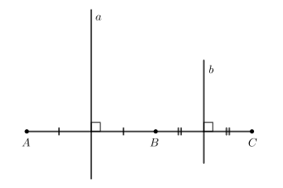
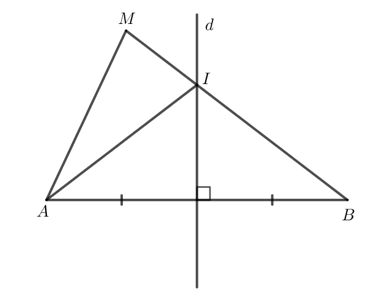
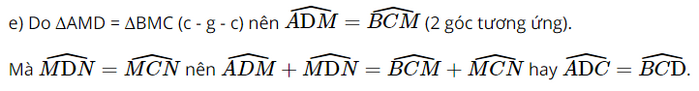Giải Toán 7 trang 103 Cánh Diều tập 2

Bài 1 trang 103 SGK Toán 7 tập 2 - Cánh Diều

Trong Hình 94, đường thẳng CD là đường trung trực của đoạn thẳng AB. Chứng minh \(\widehat {CAD} = \widehat {CBD}\).

Phương pháp:

Chứng minh \(\widehat {CAD} = \widehat {CBD}\) bằng cách chứng minh \(\widehat {CAB} - \widehat {DAB} = \widehat {CBA} - \widehat {DBA}\).

Lời giải:

Gọi H là giao điểm của CD và AB.

Do C thuộc đường trung trực của đoạn thẳng AB nên CA = CB.

Do D thuộc đường trung trực của đoạn thẳng AB nên DA = DB.

Xét ∆CHA vuông tại H và ∆CHB vuông tại H có:

CH chung.

CA = CB (chứng minh trên).

CA = CB (chứng minh trên).

Do đó ∆CHA = ∆CHB (cạnh huyền - cạnh góc vuông).

Bài 2 trang 103 SGK Toán 7 tập 2 - Cánh Diều

Trong Hình 95, đường thẳng a là đường trung trực của hai đoạn thẳng AB và CD. Chứng minh:

a) AB // CD;

b) \(\Delta MNC = \Delta MND;\)

c) \(\widehat {AMD} = \widehat {BMC}\);

d) \(AD = BC,\widehat A = \widehat B\);

e) \(\widehat {ADC} = \widehat {BCD}\).

Phương pháp:

a) Chứng minh AB // CD bằng cách dựa vào đường thẳng a là đường trung trực của cả hai đoạn thẳng AB và CD.

b) Chứng minh \(\Delta MNC = \Delta MND\) theo trường hợp cạnh huyền – cạnh góc vuông.

c) Dựa vào kết quả của phần b) để chứng minh \(\widehat {AMD} = \widehat {BMC}\).

d) Chứng minh \(AD = BC,\widehat A = \widehat B\) dựa vào cách chứng minh \(\Delta MAD = \Delta MBC\).

e) Chứng minh \(\widehat {ADC} = \widehat {BCD}\) dựa vào kết quả của phần d).

Lời giải:

a) Do a là đường trung trực của cả hai đoạn thẳng AB và CD nên a ⊥ AB và a ⊥ CD.

Do đó AB // CD.

b) Xét ∆MNC vuông tại N và ∆MND vuông tại N có:

MN chung.

NC = ND (theo giả thiết).

Do đó ∆MNC = ∆MND (2 cạnh góc vuông).

Bài 3 trang 103 SGK Toán 7 tập 2 - Cánh Diều

Cho ba điểm A, B, C thẳng hàng, điểm B nằm giữa hai điểm A và C. Gọi a và b lần lượt là đường trung trực của các đoạn thẳng AB và BC. Chứng minh a // b.

Phương pháp:

Hai đường thẳng không cắt nhau cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.

Lời giải:

a là đường trung trực của đoạn thẳng AB nên a vuông góc với AB tại trung điểm của AB.

b là đường trung trực của đoạn thẳng BC nên b vuông góc với BC tại trung điểm của BC.

Do A, B, C thẳng hàng và B nằm giữa A và C nên trung điểm của đoạn thẳng AB và trung điểm của đoạn thẳng BC không trùng nhau.

Do đó a // b.

Bài 4 trang 103 SGK Toán 7 tập 2 - Cánh Diều

Cho đường thẳng d là đường trung trực của đoạn thẳng AB. Điểm M không thuộc đường thẳng d và đoạn thẳng AB sao cho đường thẳng d cắt đoạn thẳng MB tại điểm I. Chứng minh:

a) \(MB = AI + IM\);                                                           

b) MA < MB.

Phương pháp:

a) Dựa vào tính chất của đường trung trực: Một điểm thuộc đường trung trực thì cách đều hai đầu mút.

b) Dựa vào tính chất trong tam giác: Tổng hai cạnh bất kì luôn lớn hơn độ dài cạnh còn lại.

Lời giải:

a) Đường thẳng d cắt MB tại I nên I thuộc đường trung trực của đoạn thẳng AB.

Do đó AI = BI.

Khi đó MB = BI + IM = AI + IM.

b) Xét trong tam giác AIM có AI + IM > MA.

Mà AI + IM = MB nên MB > MA.

Sachbaitap.com