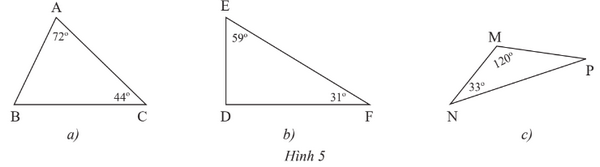
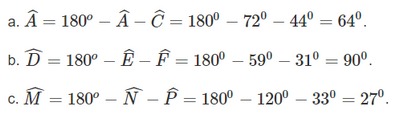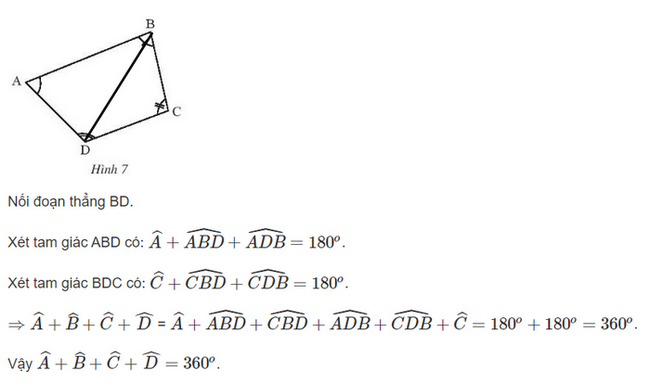Giải Toán 7 trang 46, 47 Chân trời sáng tạo tập 2

Bài 1 trang 46 SGK Toán 7 tập 2 - Chân trời sáng tạo

Tìm số đo các góc chưa biết của các tam giác trong Hình 5.

Phương pháp:

Sử dụng định lí về tổng các góc trong tam giác

Lời giải:

Bài 2 trang 47 SGK Toán 7 tập 2 - Chân trời sáng tạo

Tính số đo x của góc trong Hình 6.

Phương pháp:

Sử dụng định lí tổng 3 góc trong tam giác

Lời giải:

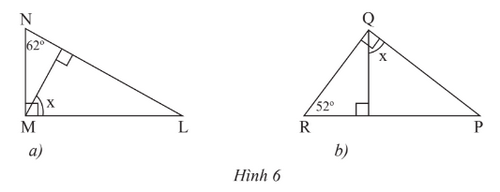
Bài 3 trang 47 SGK Toán 7 tập 2 - Chân trời sáng tạo

Hãy chia tứ giác ABCD trong Hình 7 thành hai tam giác để tính tổng số đo của bốn góc \(\widehat A\),\(\widehat B\),\(\widehat C\),\(\widehat D\).

Phương pháp:

Ta chia tứ giác thành 2 tam giác 

Áp dụng định lí tổng ba góc trong một tam giác

Lời giải:

Bài 4 trang 47 SGK Toán 7 tập 2 - Chân trời sáng tạo

Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của tam giác?

a) 4cm; 5cm; 7cm

b) 2cm; 4cm; 6cm

c) 3cm; 4cm; 8cm

Phương pháp:

Khi kiểm tra 3 đoạn thẳng có thỏa mãn bất đẳng thức tam giác không, để nhanh gọn, ta chỉ cần kiểm tra tổng độ dài của 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất hay không

Lời giải:

a) 5 - 4 < 7 < 4 + 5.

b) 2+ 4 = 6.

c) 3 + 4 < 8.

Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba câu a) 4cm, 5cm, 7cm có thể là độ dài ba cạnh của một tam giác.

Bài 5 trang 47 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho tam giác ABC có BC = 1cm, AB = 4cm. Tìm độ dài cạnh AC, biết rằng độ dài này là một số nguyên xăngtimét.

Phương pháp:

Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài 2 cạnh còn lại: b – c < a < b + c ( với a, b, c là độ dài 3 cạnh của tam giác)

Kết hợp điều kiện độ dài cạnh CA là số nguyên

Lời giải:

Áp dụng đính lí về độ dài 3 cạnh của một tam giác ta có: 4 - 1 < AC <  4 + 1, hay 3 < AC < 5.

Vì độ đài AC là một số nguyên, nên độ dài AC có thể là: 4.

Thử lại giá trị vừa tìm được 5 < 3 + 4 thỏa mãn định lí.

Vậy độ dài AC = 4cm.

Bài 6 trang 47 SGK Toán 7 tập 2 - Chân trời sáng tạo

Trong một trường học, người ta bắt đầu đánh dấu ba khu vực A, B, C là ba đỉnh của một tam giác, biết các khoảng cách AC = 15m, AB = 45m

a) Nếu đặt ở khu vực C một thiết bị phát wifi có bán kính hoạt động 30m thì tại khu vực B có nhận được tín hiệu không? Vì sao?

b) Cũng câu hỏi như trên với thiết bị phát wifi có bán kính hoạt động 60m.

Phương pháp:

Ta áp dụng bất đẳng thức tam giác: 

AB - AC < BC < AB + AC

Lời giải:

Áp dụng định lí về độ dài 3 cạnh của một tam giác có: 45 - 15 < BC < 45 + 15, hay 30 < BC < 60.

a) Nếu đặt ở khu vực C một thiết bị phát wifi có bán kính hoạt động 30 m thì khu vực B không nhận được tín hiệu vì BC > 30 m.

b) Nếu đặt ở C một thiết bị phát wifi có bán kính hoạt động 60 m thì khu vực B nhận được tín hiệu vì BC < 60 m.

Sachbaitap.com