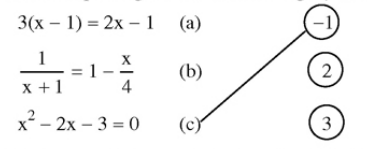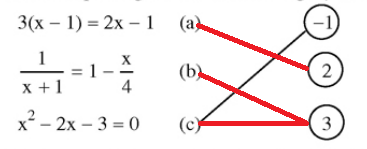Bài 1, 2, 3, 4, 5 trang 6, 7 SGK Toán 8 tập 2 - Mở đầu về phương trìnhGiải bài 1, 2, 3, 4 trang 6, bài 5 trang 7 SGK Toán lớp 8 tập 2 bài 1 Mở đầu về phương trình. Bài 3. Xét phương trình x + 1 = 1 + x. Ta thấy mọi số đều là nghiệm của nó. Người ta còn nói: Phương trình này nghiệm đúng với mọi x. Hãy cho biết tập nghiệm của phương trình đó. Bài 1 trang 6 SGK Toán lớp 8 tập 2 Câu hỏi: Với mỗi phương trình sau, hãy xét xem x = -1 có là nghiệm của nó không: a) 4x - 1 = 3x - 2; b) x + 1 = 2(x - 3); c) 2(x + 1) + 3 = 2 - x Phương pháp: - Nếu khi thay \(x = -1\) vào hai vế của phương trình ta được kết quả của hai vế bằng nhau thì \(x = -1\) là nghiệm của phương trình đó. Lời giải: Thay giá trị x = -1 vào từng vế của phương trình, ta được: a) Vế trái = 4x - 1 = 4(-1) - 1 = -5 Vế phải = 3x - 2 = 3(-1) - 2 = -5 Vế trái = Vế phải nên x = -1 là nghiệm của phương trình. b) Vế trái = x + 1 = -1 + 1 = 0 Vế phải = 2(x - 3) = 2(-1 - 3) = -8 Vế trái ≠ Vế phải nên x = -1 không là nghiệm của phương trình. c) Vế trái = 2(x + 1) + 3 = 2( -1 + 1) + 3 = 3 Vế phải = 2 - x = 2 - (-1) = 3 Vế trái = Vế phải nên x = -1 là nghiệm của phương trình. Bài 2 trang 6 SGK Toán lớp 8 tập 2 Câu hỏi: Trong các giá trị t = -1, t = 0 và t = 1, giá trị nào là nghiệm của phương trình: (t + 2)2 = 3t + 4? Phương pháp: Thay lần lượt các giá trị của t vào hai vế của phương trình ta được kết quả hai vế bằng nhau thì giá trị đó là nghiệm của phương trình. Lời giải: Lần lượt thay các giá trị của t vào hai vế của phương trình ta được: - Tại t = -1 : Vế trái = (t + 2)2 = (–1 + 2)2 = 1 Vế phải = 3t + 4 = 3.(–1) + 4 = 1 ⇒ t = – 1 là nghiệm của phương trình (t + 2)2 = 3t + 4. - Tại t = 0 Vế trái = (t + 2)2 = (0 + 2)2 = 4 Vế phải = 3t + 4 = 3.0 + 4 = 4 ⇒ t = 0 là nghiệm của phương trình (t + 2)2 = 3t + 4. - Tại t = 1 Vế trái = (t + 2)2 = (1 + 2)2 = 9 Vế phải = 3t + 4 = 3.1 + 4 = 7 ⇒ t = 1 không là nghiệm của phương trình (t + 2)2 = 3t + 4. Vậy t = –1, t = 0 là nghiệm của phương trình đã cho. Bài 3 trang 6 SGK Toán lớp 8 tập 2 Câu hỏi: Xét phương trình x + 1 = 1 + x. Ta thấy mọi số đều là nghiệm của nó. Người ta còn nói: Phương trình này nghiệm đúng với mọi x. Hãy cho biết tập nghiệm của phương trình đó. Phương pháp: Áp dụng định nghĩa: - Nghiệm của phương trình là giá trị của ẩn \(x\) thoả mãn phương trình. - Tập nghiệm của phương trình là tập hợp tất cả các nghiệm của phương trình đó. Lời giải: Vì phương trình \(x + 1 = 1 + x\) nghiệm đúng với mọi \(x \in \mathbb R\). Vậy tập nghiệm của phương trình trên là: \(S = \mathbb R.\) Bài 4 trang 7 SGK Toán lớp 8 tập 2 Câu hỏi: Nối mỗi phương trình sau với các nghiệm của nó:
Lời giải: *) Xét phương trình \(3(x-1)=2x-1\;\;\;\;\;(1)\) +) Thay \(x=-1\) vào vế trái và vế phải của phương trình (1) ta được: \(\eqalign{ \( - 6 \ne - 3 \Rightarrow VT \ne VP\) Vậy \(x=-1\) không là nghiệm của phương trình (1) +) Thay \(x=2\) vào vế trái và vế phải của phương trình (1) ta được: \(\eqalign{ \(3 = 3 \Rightarrow VT = VP\) Vậy \(x=2\) là nghiệm của phương trình (1) +) Thay \(x=3\) vào vế trái và vế phải của phương trình (1) ta được: \(\eqalign{ \(6 \ne 5 \Rightarrow VT \ne VP\) Vậy \(x=3\) không là nghiệm của phương trình (1) *) Xét phương trình \(\dfrac{1}{{x + 1}} = 1 - \dfrac{x}{4}\;\;\;\;\;(2)\) +) Với \(x=-1\) thì phương trình (2) không xác định nên \(x=-1\) không là nghiệm của phương trình (2) +) Thay \(x=2\) vào vế trái và vế phải của phương trình (2) ta được: \(\eqalign{ \(\dfrac{1}{3} \ne \dfrac{1}{2} \Rightarrow VT \ne VP\) Vậy \(x=2\) không là nghiệm của phương trình (2) +) Thay \(x=3\) vào vế trái và vế phải của phương trình (2) ta được: \(\eqalign{ \(\dfrac{1}{4} = \dfrac{1}{4} \Rightarrow VT = VP\) Vậy \(x=3\) là nghiệm của phương trình (2) *) Xét phương trình \({x^2} - 2x - 3 = 0\,\,\,\,\,\,\,\,\,\,\,\,\,(3)\) +) Thay \(x=-1\) vào vế trái và vế phải của phương trình (3) ta được: \(\eqalign{ \(0 = 0 \Rightarrow VT = VP\) Vậy \(x=-1\) là nghiệm của phương trình (3) +) Thay \(x=2\) vào vế trái và vế phải của phương trình (3) ta được: \(\eqalign{ \( - 3 \ne 0 \Rightarrow VT \ne VP\) Vậy \(x=2\) không là nghiệm của phương trình (3) +) Thay \(x=3\) vào vế trái và vế phải của phương trình (3) ta được: \(\eqalign{ \(0 = 0 \Rightarrow VT = VP\) Vậy \(x=3\) là nghiệm của phương trình (3) Ta nối như sau:
Bài 5 trang 7 SGK Toán lớp 8 tập 2 Câu hỏi: Hai phương trình x = 0 và x(x - 1) = 0 có tương đương không? Vì sao? Lời giải: Phương trình \(x = 0\) có tập nghiệm \({S_1} = {\rm{\{ }}0\} \). Xét phương trình \(x(x - 1) = 0\). Ta có một tích bằng \(0\) khi một trong hai thừa số bằng \(0\) tức là: \(x(x - 1) = 0\) khi \(x = 0\) hoặc \(x = 1\). Vậy phương trình \(x(x - 1) = 0\) có tập nghiệm \({S_2} = {\rm{\{ }}0;1\} \) Vì \({S_1} \ne {S_2}\) nên hai phương trình không tương đương. Sachbaitap.com
Xem thêm tại đây:
Chương III. Phương trình bậc nhất một ẩn
|
-

Bài 6, 7, 8, 9 trang 9, 10 SGK Toán 8 tập 2 - Phương trình bậc nhất một ẩn và cách giải
Giải bài 6 trang 9, bài 7, 8, 9 trang 10 SGK Toán lớp 8 tập 2 bài 2 Phương trình bậc nhất một ẩn và cách giải. Bài 7. Hãy chỉ ra các phương trình bậc nhất trong các phương trình sau:
-

Bài 10, 11, 12, 13 trang 12, 13 SGK Toán 8 tập 2 - Phương trình đưa được về dạng ax + b = 0
Giải bài 10 trang 12, bài 11, 12, 13 trang 13 SGK Toán lớp 8 tập 2 bài 3 Phương trình đưa được về dạng ax + b = 0. Bài 1. Tìm chỗ sai và sửa lại các bài giải sau cho đúng:
-

Bài 14, 15, 16, 17, 18, 19, 20 trang 13, 14 SGK Toán 8 tập 2 - luyện tập
Giải bài 14, 15, 16 trang 13, bài 17, 18, 19, 20 trang 14 SGK Toán lớp 8 tập 2 bài 3 luyện tập. Bài 19: Viết phương trình ẩn x rồi tính x (mét), trong mỗi hình dưới đây (h.4) (S là diện tích của hình):
-

Bài 21, 22, 23, 24, 25, 26 trang 17 SGK Toán 8 tập 2 - Phương trình tích
Giải bài 21,22,23,24,25,26 trang 17, SGK Toán lớp 8 tập 2 bài 4 phương trình tích- luyện tập. Bài 26: Giáo viên chuẩn bị 4 đề toán về giải phương trình, đánh số từ 1 đến 4.

 Tải ngay
Tải ngay