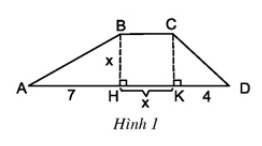
Bài 6, 7, 8, 9 trang 9, 10 SGK Toán 8 tập 2 - Phương trình bậc nhất một ẩn và cách giải

Bài 6 trang 9 SGK Toán lớp 8 tập 2

Câu hỏi:

Tính diện tích S của hình thang ABCD (h.1) theo x bằng hai cách:

1) Tính theo công thức: S = BH x (BC + DA) : 2

2) S = S_ABH + S_BCKH + S_CKD

Sau đó, sử dụng giả thiết S = 20 để thu được hai phương trình tương đương với nhau. Trong hai phương trình ấy, có phương trình nào là phương trình bậc nhất không?

Lời giải:

Gọi S là diện tích hình thang ABCD. 

1) Theo công thức

                    \(S =  \dfrac{BH(BC+DA)}{2}\)

Ta có: \(AD = AH + HK + KD\)

\(\Rightarrow AD = 7 + x + 4 = 11 + x\)

Có \(BH\bot HK, CK\bot HK\) (giả thiết)

Mà \(BC//HK\) (vì \(ABCD\) là hình thang)

Do đó \(BH\bot BC, CK\bot BC\)

Tứ giác \(BCKH\) có bốn góc vuông nên \(BCKH\) là hình chữ nhật

Mặt khác: \(BH=HK=x\) (giả thiết) nên \(BCKH\) là hình vuông

\( \Rightarrow BH = BC =CK=KH= x\)

Thay \(BH=x\), \(BC=x\), \(DA=11+x\) vào biểu thức tính \(S\) ta được:

\(S = \dfrac{{x\left( {x + 11 + x} \right)}}{2} = \dfrac{{x(11 + 2x)}}{2}\)\(\,=\dfrac{{11x + 2{x^2}}}{2}\) 

2) Ta có: 

\(\eqalign{
& S = {S_{ABH}} + {S_{BCKH}} + {S_{CKD}} \cr
& \,\,\,\,\, = {1 \over 2}BH.AH + BH.HK + {1 \over 2}CK.KD \cr
& \,\,\,\,\, = {1 \over 2}x.7 + x.x + {1 \over 2}.x.4 \cr
& \,\,\,\,\, = {7 \over 2}x + {x^2} + 2x \cr 
& \,\,\,\,\, =x^2+{11 \over 2}x \cr} \)

Vậy \(S = 20\) ta có hai phương trình: 

  \(\dfrac{{11x + 2{x^2}}}{2}= 20\)          (1)

  \( \dfrac{11}{2}x + x^2  = 20  \)       (2)

Hai phương trình trên tương đương và cả hai phương trình không có phương trình nào là phương trình bậc nhất.

Bài 7 trang 10 SGK Toán lớp 8 tập 2

Câu hỏi:

Hãy chỉ ra các phương trình bậc nhất trong các phương trình sau:

a) 1 + x = 0

b) x + x² = 0

c) 1 – 2t = 0

d) 3y = 0

e) 0x – 3 = 0.

Phương pháp:

Phương trình có dạng \(ax+b=0\), với \(a\) và \(b\) là hai số đã cho và \(a\ne0\), được gọi là phương trình bậc nhất một ẩn.

Lời giải:

Phương trình dạng ax+ b= 0, với a, b là hai số đã cho và a ≠ 0 , được gọi là phương trình bậc nhất một ẩn.

+ Phương trình 1 + x = 0 là phương trình bậc nhất với a = 1 ; b = 1.

+ Phương trình x + x² = 0 không phải phương trình bậc nhất vì có chứa x² bậc hai.

+ Phương trình 1 – 2t = 0 là phương trình bậc nhất ẩn t với a = -2 và b = 1.

+ Phương trình 3y = 0 là phương trình bậc nhất ẩn y với a = 3 và b = 0.

+ Phương trình 0x – 3 = 0 không phải phương trình bậc nhất vì hệ số bậc nhất a = 0.

Bài 8 trang 10 SGK Toán lớp 8 tập 2

Câu hỏi:

 Giải các phương trình:

a) 4x – 20 = 0

b) 2x + x + 12 = 0

c) x – 5 = 3 – x

d) 7 – 3x = 9 – x

Lời giải:

a) \(4x - 20 = 0 \)

\(\Leftrightarrow  4x = 20  \)

\( \Leftrightarrow x = \dfrac{20} {4}\)

\(\Leftrightarrow  x = 5\)

Vậy phương trình có nghiệm duy nhất \(x = 5\).

b) \(2x + x + 12 = 0\)

\( \Leftrightarrow  3x + 12 = 0\)

\( \Leftrightarrow 3x = -12\)

\( \Leftrightarrow x = \dfrac{{ - 12}}{3}\)

\( \Leftrightarrow x = - 4\)

Vậy phương trình đã cho có nghiệm duy nhất \(x = - 4\)

c) \(x - 5 = 3 - x\)

\( \Leftrightarrow  x + x = 3+5\)

\( \Leftrightarrow  2x = 8 \)

\( \Leftrightarrow x = \dfrac{8}{2}\)

\( \Leftrightarrow  x = 4\)

Vậy phương trình có nghiệm duy nhất \(x = 4\)

d) \(7 - 3x = 9 - x\)

\( \Leftrightarrow  -3x+x = 9 -7\)

\( \Leftrightarrow  -2x = 2\)

\( \Leftrightarrow x = \dfrac{2}{{ - 2}}\)

\( \Leftrightarrow  x = -1\)

Vậy phương trình có nghiệm duy nhất \(x = -1\).

Bài 9 trang 10 SGK Toán lớp 8 tập 2

Câu hỏi:

Giải các phương trình sau, viết số gần đúng của mỗi nghiệm ở dạng số thập phân bằng cách làm tròn đến hàng phần trăm.

a) 3x – 11 = 0

b) 12 + 7x = 0

c) 10 – 4x = 2x – 3

Lời giải:

 a) 

\(3x -11 = 0\)

\( \Leftrightarrow  3x = 11\)

\( \Leftrightarrow  x =  \dfrac{11}{3}\) 

\( \Leftrightarrow  x  \approx 3, 67\)

Vậy nghiệm gần đúng của phương trình là \(x \approx 3,67\).

b)

\(12 + 7x = 0\)

\( \Leftrightarrow  7x = -12 \)

\( \Leftrightarrow  x = \dfrac{-12}{7}\)

\( \Leftrightarrow  x  \approx -1,71\)

Vậy nghiệm gần đúng của phương trình là \(x \approx  - 1,71\).

c)

\(10 - 4x = 2x - 3\)

\( \Leftrightarrow  -4x - 2x = -3 - 10\) 

\( \Leftrightarrow -6x = -13\)

\( \Leftrightarrow  x =  \dfrac{-13}{-6}\)

\( \Leftrightarrow  x \approx  2,17\)

Vậy nghiệm gần đúng của phương trình là \(x \approx 2,17\).

Sachbaitap.com