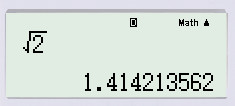
Bài 1, 2, 3, 4, 5 trang 6, 7 SGK Toán 9 tập 1 - Căn bậc haiGiải bài 1, 2, 3 trang 6, bài 4, 5 trang 7 sách giáo khoa Toán lớp 9 tập 1 - bài căn bậc hai. Bài 1 Tìm căn bậc hai số học của mỗi số sau rồi suy ra căn bậc hai của chúng 121; 144; 169; 225; 256; 324; 361; 400. Bài 1 trang 6 SGK Toán lớp 9 tập 1 Câu hỏi: Tìm căn bậc hai số học của mỗi số sau rồi suy ra căn bậc hai của chúng 121; 144; 169; 225; 256; 324; 361; 400. Phương pháp: +) Căn bậc hai số học của \(a\) là \( \sqrt{a} \) với \(a>0\). +) Số dương \(a\) có đúng hai căn bậc hai là hai số đối nhau: Số dương kí hiệu là \( \sqrt{a}\) và số âm kí hiệu là \(- \sqrt{a}\). Lời giải: Ta có: + \(\sqrt{121}\) có căn bậc hai số học là \(11\) (vì \(11>0\) và \(11^2=121\) ) \(\Rightarrow 121\) có hai căn bậc hai là \(11\) và \(-11\). + \(\sqrt{144}\) có căn bậc hai số học là \(12\) (vì \(12>0\) và \(12^2=144\) ) \(\Rightarrow 144\) có hai căn bậc hai là \(12\) và \(-12\). + \(\sqrt{169}\) có căn bậc hai số học là \(13\) (vì \(13>0\) và \(13^2=169\) ) \(\Rightarrow 169\) có hai căn bậc hai là \(13\) và \(-13\). + \(\sqrt{225}\) có căn bậc hai số học là \(15\) (vì \(15>0\) và \(15^2=225\) ) \(\Rightarrow 225\) có hai căn bậc hai là \(15\) và \(-15\). + \(\sqrt{256}\) có căn bậc hai số học là \(16\) (vì \(16>0\) và \(16^2=256\) ) \(\Rightarrow 256\) có hai căn bậc hai là \(16\) và \(-16\). + \(\sqrt{324}\) có căn bậc hai số học là \(18\) (vì \(18>0\) và \(18^2=324\) ) \(\Rightarrow 324 \) có hai căn bậc hai là \(18\) và \(-18\). + \(\sqrt{361}\) có căn bậc hai số học là \(19\) (vì \(19>0\) và \(19^2=361\) ) \(\Rightarrow 361\) có hai căn bậc hai là \(19\) và \(-19\). + \(\sqrt{400}\) có căn bậc hai số học là \(20\) (vì \(20>0\) và \(20^2=400\) ) \(\Rightarrow 400 \) có hai căn bậc hai là \(20\) và \(-20\). Bài 2 trang 6 SGK Toán lớp 9 tập 1 Câu hỏi: So sánh: a. \(2\) và \(\sqrt{3}\) b. \(6\) và \(\sqrt{41}\) c. \(7\) và \(\sqrt{47}\) Phương pháp: +) Sử dụng định lí so sánh hai căn bậc hai số học: Với hai số \(a\) và \(b\) không âm ta có: \[ a<b\Leftrightarrow \sqrt{a}<\sqrt{b}\] Lời giải: a. Ta có: \(2=\sqrt 4\) Vì \(4>3 \Leftrightarrow \sqrt{4}>\sqrt{3} \Leftrightarrow 2>\sqrt{3}\). Vậy \(2>\sqrt{3}\). b. Ta có: \(6=\sqrt {36}\) Vì \(36< 41 \Leftrightarrow \sqrt{36} < \sqrt{41} \Leftrightarrow 6 < \sqrt {41}\) Vậy \(6<\sqrt{41}\). c. Ta có: \(7=\sqrt {49}\) Vì \(49>47 \Leftrightarrow \sqrt{49}>\sqrt{47} \Leftrightarrow 7>\sqrt{47}\). Vậy \(7>\sqrt{47}\). Bài 3 trang 6 SGK Toán lớp 9 tập 1 Câu hỏi: Dùng máy tính bỏ túi, tính giá trị gần đúng của nghiệm mỗi phương trình sau (làm tròn đến số thập phân thứ ba). a) x2 = 2; b) x2 = 3; c) x2 = 3,5; d) x2 = 4,12; Hướng dẫn: Nghiệm của phương trình x2 = a ( với a ≥ 0) là các căn bậc hai của a. Lời giải: a. Ta có: \({x^2} = 2 \Leftrightarrow x = \pm \sqrt 2 \) Bấm máy tính ta được: \(x\approx \pm 1,414\)
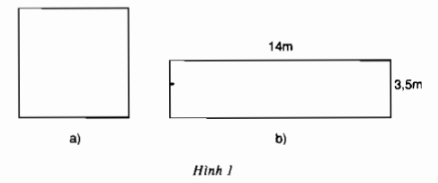
b. Ta có: \({x^2} = 3 \Leftrightarrow x = \pm \sqrt 3 \) Tính bằng máy tính ta được: \( x \approx \pm 1,732\) c. Ta có: \({x^2} = 3,5 \Leftrightarrow x = \pm \sqrt {3,5} \) Tính bằng máy tính ta được: \(x \approx \pm 1,871\) d. Ta có: \({x^2} = 4,12 \Leftrightarrow x = \pm \sqrt {4,12} \) Tính bằng máy tính ta được: \(x \approx \pm 2,030\) Bài 4 trang 7 SGK Toán lớp 9 tập 1 Câu hỏi: Tìm số x không âm, biết: a) \(\sqrt{x}=15\); b) \(2\sqrt{x}=14\); c) \(\sqrt{x}<\sqrt{2}\); d) \(\sqrt{2x}<4\). Phương pháp: - Sử dụng công thức \(a = (\sqrt{a})^2\) với \(a ≥ 0\). - Sử dụng phương pháp bình phương hai vế: \(\sqrt{A}=B \Leftrightarrow A=B^2 \), với \(A\), \(B \ge 0 \). Lời giải: a. Vì \(x\ge 0\) nên \(\sqrt x = 15 \Rightarrow \left( {\sqrt x } \right)^2 = {\left( {15} \right)^2}\) \(\Leftrightarrow x = 225\) Vậy \(x=225.\) b. Vì \(x\ge 0\) nên \(2\sqrt x = 14 \Leftrightarrow \sqrt x = 7 \) \( \Leftrightarrow \left( {\sqrt x } \right)^2 = { 7 ^2} \) \(\Leftrightarrow x = 49\) Vậy \(x=49\) c. \(\sqrt x < \sqrt 2 \Leftrightarrow x<2\) Kết hợp với \(x\ge 0\) ta có \( 0 \le x < 2\) Vậy \( 0 \le x < 2\) d. Với \(x\ge 0\) ta có \(\sqrt {2x} < 4\) \(\Leftrightarrow \sqrt {2x} < \sqrt {16}\) \(\Leftrightarrow 2x < 16\) \(\Leftrightarrow x<8\) Kết hợp điều kiện \(x\ge 0\) ta có: \( 0 \le x < 8\) Bài 5 trang 7 SGK Toán lớp 9 tập 1 Câu hỏi: Đố. Tính cạnh một hình vuông, biết diện tích của nó bằng diện tích của một hình chữ nhật có chiều rộng 3,5m và chiều dài 14m.
Phương pháp: - Công thức tính diện tích hình vuông cạnh \(a\) là \(S={a^2}\). - Công thức tính diện tích hình chữ nhật có chiều dài và chiều rộng lần lượt là \(a; b\) là \( S=a.b\) Lời giải: Gọi \(x\) (m) là độ dài hình vuông, \(x > 0\) . Diện tích của hình vuông là: \(x^2 \, (m^2)\) Diện tích của hình chữ nhật là: \(3,5.14 = 49\) \(m^2\). Theo đề bài, diện tích của hình vuông bằng diện tích của hình chữ nhật, nên ta có: \( x^2 =49 \Leftrightarrow x=\pm \sqrt {49} \Leftrightarrow x = \pm 7\). Vì \(x > 0\) nên \(x = 7\). Vậy độ dài cạnh hình vuông là \(7m\). Sachbaitap.com
Xem thêm tại đây:
Bài 1. Căn bậc hai
|
-

Bài 6, 7, 8, 9, 10 trang 10, 11 SGK Toán 9 tập 1 - Căn thức bậc hai và hằng đẳng thức
Giải bài 6, 7, 8 trang 10, bài 9, 10 trang 11 sách giáo khoa Toán lớp 9 tập 1 bài Căn thức bậc hai và hằng đẳng thức. Bài 6 Với giá trị nào của a thì mỗi căn thức sau có nghĩa.
-

Bài 11, 12, 13, 14, 15, 16 trang 11, 12 SGK Toán 9 tập 1 - Luyện tập
Giải bài 11, 12, 13, 14, 15 trang 11, bài 16 trang 12 sách giáo khoa Toán lớp 9 tập 1 bài Luyện tập. Bài 16 Đố. Hãy tìm chỗ sai trong phép chứng minh "Con muỗi nặng bằng con voi" dưới đây.

 Tải ngay
Tải ngay