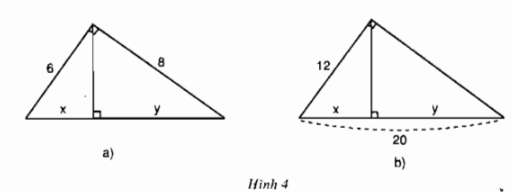
Bài 1, 2, 3, 4 trang 68, 69 SGK Toán 9 tập 1 - Một số hệ thức về cạnh và đường cao trong tam giác vuôngGiải bài 1, 2 trang 68; bài 3, 4 trang 69 sách giáo khoa Toán lớp 9 tập 1 bài Một số hệ thức về cạnh và đường cao trong tam giác vuông. Bài 1 trang 68 SGK Toán lớp 9 tập 1 Câu hỏi: Hãy tính \(x\) và \(y\) trong mỗi hình sau (hình \(4a,\ b)\):
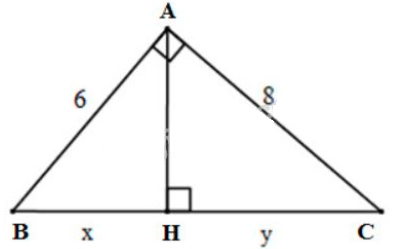
Lời giải: a) Đặt tên các đỉnh của tam giác như hình dưới:
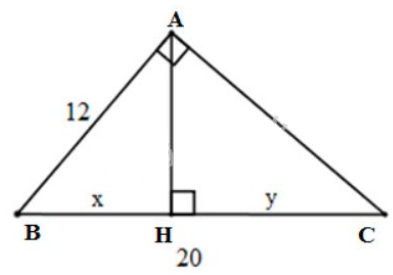
Áp dụng định lí Pytago vào \(\Delta{ABC}\) vuông tại \(A\), ta có: \(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\) Áp dụng hệ thức lượng vào\(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\), ta có: \(AB^2=BC.BH\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6\) Lại có \(HC=BC-BH=10-3,6=6,4\) Vậy \(x =BH= 3,6\); \(y=HC = 6,4\). b) Đặt tên các đỉnh của tam giác như hình dưới
Áp dụng hệ thức lượng vào \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\), ta có: \(AB^2=BH.BC \Leftrightarrow 12^2=20.x \Rightarrow x=\dfrac{12^2}{20}=7,2\) Lại có: \(HC=BC-BH=20-7,2=12,8\) Vậy \(x=BH = 7,2;\) \(y=HC = 12,8\). Bài 2 trang 68 SGK Toán lớp 9 tập 1 Câu hỏi: Hãy tính \(x\) và \(y\) trong hình dưới đây:
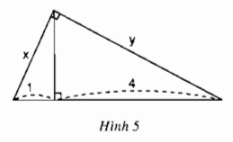
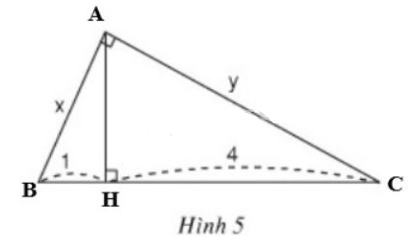
Phương pháp: +) Sử dụng định lí Pytago trong tam giác vuông: \(\Delta{ABC}\) vuông tại \(A\), khi đó: \(BC^2=AC^2+AB^2\). +) Sử dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền: \(b^2=a.b',\ c^2=a.c'\) Lời giải: Đặt tên các đỉnh như hình vẽ:
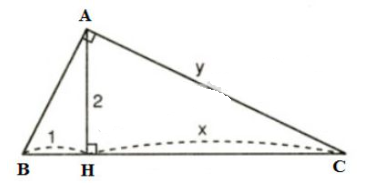
Ta có: \(BC=BH + HC=1+4=5\). Xét \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\), áp dụng hệ thức lượng trong tam giác vuông, ta có: \(AB^2=BH.BC \Leftrightarrow x^2=1.5\) (với \(x > 0)\) \(\Leftrightarrow x^2=5\) \(\Leftrightarrow x=\sqrt 5\). \(AC^2=CH.BC \Leftrightarrow y^2=4.5\) (với \(y> 0)\) \(\Leftrightarrow y^2=20\) \(\Leftrightarrow y=\sqrt{20}\) \(\Leftrightarrow y=2\sqrt{5}\). Vậy \(x= \sqrt 5\), \(y=2\sqrt 5\). Bài 3 trang 69 SGK Toán lớp 9 tập 1 Câu hỏi: Hãy tính \(x\) và \(y\) trong hình sau:
Lời giải: Đặt tên các điểm như trong hình:
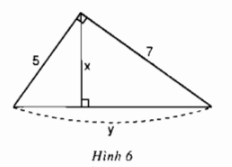
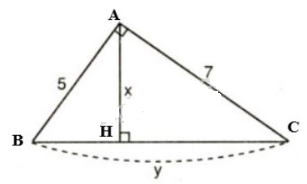
Xét \(\Delta{ABC}\) vuông tại \(A\). Theo định lí Pytago, ta có: \(BC^2=AB^2+AC^2\) \(\Leftrightarrow y^2=5^2+7^2\) \(\Leftrightarrow y^2=74\) \(\Leftrightarrow y=\sqrt{74}\) Cách 1: \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\), áp dụng công thức \(b.c=h.a\), ta được: \(AB.AC=AH.BC \) \(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{5.7}{\sqrt{74}}=\dfrac{35\sqrt{74}}{74}\). Cách 2: Áp dụng hệ thức liên quan đến đường cao trong tam giác vuông, ta có: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\) \(\Leftrightarrow \dfrac{1}{x^2}=\dfrac{1}{5^2}+\dfrac{1}{7^2}\) \(\Leftrightarrow \dfrac{1}{x^2}=\dfrac{74}{1225}\) \(\Leftrightarrow x=\sqrt{\dfrac{1225}{74}}\) \( \Leftrightarrow x=\dfrac{35\sqrt{74}}{74}\) Vậy \(\ x=\dfrac{35\sqrt{74}}{74}, \, y=\sqrt {74}\) Bài 4 trang 69 SGK Toán lớp 9 tập 1 Câu hỏi: Hãy tính \(x\) và \(y\) trong hình sau:
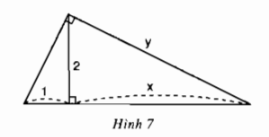
Phương pháp: +) Sử dụng hệ thức liên quan đến đường cao và hình chiếu \(h^2=b'.c'\). Biết \(h,\ c'\) tính được \(b'\). +) Tính độ dài cạnh huyền: \(a=b'+c'\). +) Sử dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền \(b^2=b'.a\). Biết \(a,\ b'\) tính được \(b\). Lời giải: Đặt tên các đỉnh của tam giác như hình bên dưới
Xét \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\). Áp dụng hệ thức liên quan đến đường cao, ta có: \(h^{2}=b'.c'\) \(\Leftrightarrow AH^{2}=HB.HC\) \(\Leftrightarrow 2^2=1.x\) \(\Rightarrow x= 4.\) Ta có: \(BC = BH+HC = 1+4=5 \) Áp dụng hệ thức \(b^{2}=b'.a\), ta có: \(AC^{2}=CH.BC\) \( \Leftrightarrow y^{2}=5. 4\) \(\Leftrightarrow y^2=20\) \(\Leftrightarrow y =\sqrt{20}=2\sqrt{5}.\) Vậy \(x=4,\ y=2\sqrt 5\). Sachbaitap.com
Xem thêm tại đây:
Bài 1. Một số hệ thức về cạnh và đường cao trong tam giác vuông
|
-

Bài 5, 6, 7, 8, 9 trang 69, 70 SGK Toán 9 tập 1 - Luyện tập
Giải bài 5, 6, 7 trang 69; bài 8, 9 trang 70 sách giáo khoa Toán lớp 9 tập 1 bài Luyện tập. Bài 5Trong tam giác vuông với các cạnh góc vuông có độ dài là 3 và 4, kẻ đường cao ứng với cạnh huyền.
-

Bài 10, 11, 12 trang 76 SGK Toán 9 tập 1 - Tỉ số lượng giác của góc nhọn
Giải bài 10, 11, 12 trang 76 sách giáo khoa Toán lớp 9 tập 1 bài Tỉ số lượng giác của góc nhọn. Bài 11Cho tam giác ABC vuông tại C, trong đó AC=0,9m, BC=1,2m. Tính các tỷ số lượng giác của góc B, từ đó suy ra các tỷ số lượng giác của góc A.
-

Bài 13, 14, 15, 16, 17 trang 77 SGK Toán 9 tập 1 - Luyện tập
Giải bài 13, 14, 15, 16, 17 trang 77 sách giáo khoa Toán lớp 9 tập 1 bài Luyện tập - Tỉ số lượng giác của góc nhọn. Bài 15 Cho tam giác ABC vuông tại A. Biết cos B = 0,8, hãy tính các tỉ số lượng giác của góc C.

 Tải ngay
Tải ngay