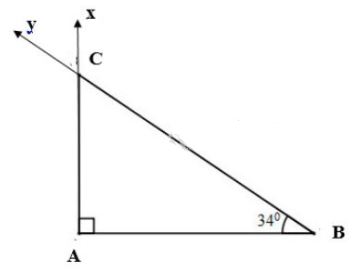
Bài 10, 11, 12 trang 76 SGK Toán 9 tập 1 - Tỉ số lượng giác của góc nhọn

Bài 10 trang 76 SGK Toán lớp 9 tập 1

Câu hỏi:

Vẽ một tam giác vuông có một góc nhọn \(34^{\circ}\) rồi viết các tỉ số lượng giác của góc \(34^{\circ}\).

Lời giải:

Vẽ tam giác \(ABC\) vuông tại \(A\) với \(\widehat{B}=34^{\circ}\).

Để vẽ được tam giác đề yêu cầu, chúng ta thực hiện các bước như sau:

B1. Vẽ đoạn thẳng \(AB\) với độ dài bất kì.

B2. Từ \(A\) dựng tia \(Ax\) vuông góc với đoạn thẳng \(AB\)

B3. Từ \(B\) dùng thước đo góc vẽ tia \(By\) sao cho góc \(ABy\) bằng \(34\) độ.

B4. \(Ax\) và \(By\) cắt nhau tại \(C\). 

B5. Nối các điểm lại với nhau ta được tam giác \(ABC\) cần dựng.

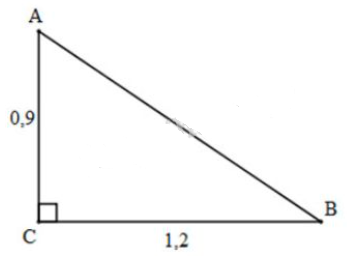
Tỉ số lượng giác của góc \(\widehat{B}=34^o\) là:

                  \(\sin 34^o=\sin B=\dfrac{AC}{BC}\)

                  \(\cos 34^o=\cos B=\dfrac{AB}{BC}\)

                  \(\tan 34^o=\tan B=\dfrac{AC}{AB}\)

                  \(\cot 34^o=\tan B=\dfrac{AB}{AC}\)

Bài 11 trang 76 SGK Toán lớp 9 tập 1

Câu hỏi:

Cho tam giác ABC vuông tại C, trong đó AC=0,9m, BC=1,2m. Tính các tỷ số lượng giác của góc B, từ đó suy ra các tỷ số lượng giác của góc A.

Phương pháp:

Lời giải:

 Xét \(\Delta{ABC}\) vuông tại \(C\), áp dụng định lí Pytago, ta có: 

            \(AB^2=CB^2+AC^2\)

        \(\Leftrightarrow AB^2=0,9^2+1,2^2\) 

        \(\Leftrightarrow AB^2=0,81+1,44=2,25\)

       \(\Leftrightarrow AB=\sqrt{2,25}=1,5m\)

Vì \(\Delta{ABC}\) vuông tại \(C\) nên góc \(B\) và \(A\) là hai góc phụ nhau. Do vậy, ta có:

         \(\sin A=\cos B=\dfrac{BC}{AB}=\dfrac{1,2}{1,5}=\dfrac{4}{5}\)

         \(\cos A=\sin B=\dfrac{AC}{AB} =\dfrac{0,9}{1,5}=\dfrac{3}{5}\)

        \(\tan A=\cot B=\dfrac{BC}{AC}=\dfrac{1,2}{0,9}=\dfrac{4}{3}\)

        \(\cot A=\tan B=\dfrac{AC}{BC}=\dfrac{0,9}{1,2}=\dfrac{3}{4}\)

Nhận xét: Với hai góc phụ nhau, ta có sin góc này bằng cosin góc kia, tan góc này bằng cotan góc kia!

Bài 12 trang 76 SGK Toán lớp 9 tập 1

Câu hỏi:

Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn \(45^{\circ}\):

\(\sin 60^{\circ}\);   \(\cos75^{\circ}\);  \(\sin52^{\circ}30'\);   \(\cot 82^{\circ}\);   \(\tan 80^{\circ}.\)

Lời giải:

Vận dụng định lý về tỉ số lượng giác của hai góc phụ nhau ta có:

             \(\sin 60^o=\cos (90^o-60^o)=\cos 30^o\)

             \(\cos 75^o=\sin (90^o-75^o)=\sin 15^o\)

             \(\sin 52^o30'=\cos (90^o-52^o 30')=\cos 37^o 30'\)

             \(\cot 82^o=\tan (90^o - 82^o)=\tan 8^o\)

             \(\tan 80^o=\cot (90^o - 80^o)=\cot 10^o\).

Cách khác:

Vì \(30^0+60^0=90^0\) nên \(\sin 60^0=\cos 30^0\) 

Vì \(75^0+15^0=90^0\) nên \(\cos 75^0=\sin 15^0\)

Vì \(52^030'+37^030'=90^0\) nên \(\sin 52^030'=\cos 37^030'\)

Vì \(82^0+8^0=90^0\) nên \(\cot 82^0=\tan 8^0\)

Vì \(80^0+10^0=90^0\) nên \(\tan 80^0=\cot 10^0\)

Sachbaitap.com