Bài 1, 2, 3 trang 44, 45 SGK Toán 9 tập 1 - Nhắc lại và bổ sung các khái niệm về hàm số

Bài 1 trang 44 SGK Toán lớp 9 tập 1

Câu hỏi:

a) Cho hàm số \(y = f(x) = \dfrac{2}{3} x\). 

Tính: \(f(-2);\)    \(f(-1);\)       \( f(0); \)     \(f(\frac{1}{2});\)    \( f(1);\)   \( f(2); \)       \(f(3)\).

b) Cho hàm số \(y = g(x) = \dfrac{2}{3} x + 3\).

Tính: \(g(-2);\)     \( g(-1);\)   \( g(0);\)     \( g(\dfrac{1}{2});\)   \( g(1);\)      \( g(2);\)    \( g(3)\).

c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến \(x\) lấy cùng một giá trị ?

Lời giải:

a) Thay các giá trị vào hàm số \(y = f(x) = \dfrac{2}{3} x\). Ta có

 \(f(-2) = \dfrac{2}{3}.(-2)=\dfrac{2.(-2)}{3}=\dfrac{-4}{3}\).

 \(f(-1) = \dfrac{2}{3}.(-1)= \dfrac{2.(-1)}{3}=\dfrac{-2}{3}\).

 \(f(0) = \dfrac{2}{3}.0=0\). 

 \(f\left (\dfrac{1}{2}\right ) =\dfrac{2}{3}.\dfrac{1}{2}=\dfrac{1}{3}\).

 \(f(1) = \dfrac{2}{3}.1=\dfrac{2}{3}\).

 \(f(2) = \dfrac{2}{3}.2=\dfrac{4}{3}\).

 \(f(3) = \dfrac{2}{3}.3=2\). 

b) Thay các giá trị vào hàm số \(y = g(x) = \dfrac{2}{3} x + 3\). Ta có

 \(g(-2) = \dfrac{2}{3}.(-2)+3= \dfrac{2.(-2)}{3}+3\\=\dfrac{-4}{3}+\dfrac{9}{3}=\dfrac{5}{3}.\)

 \(g(-1) = \dfrac{2}{3}.(-1)+3 = \dfrac{2.(-1)}{3}+3\\= \dfrac{-2}{3}+\dfrac{9}{3}=\dfrac{7}{3}.\)

 \(g(0) = \dfrac{2}{3}.0+3= \dfrac{2.0}{3}+3=0+3=3.\)

 \(g\left ( \dfrac{1}{2} \right ) = \dfrac{2}{3}. \dfrac{1}{2} +3\\=\dfrac{1}{3}+3=\dfrac{1}{3}+\dfrac{9}{3}=\dfrac{10}{3}.\)

 \(g(1) = \dfrac{2}{3}.1+3=\dfrac{2}{3}+3\\=\dfrac{2}{3}+\dfrac{9}{3}=\dfrac{11}{3}.\)

 \(g(2) = \dfrac{2}{3}.2+3=\dfrac{2.2}{3}+3=\dfrac{4}{3}+3\\=\dfrac{4}{3}+\dfrac{9}{3}=\dfrac{13}{3}\)

 \(g(3) = \dfrac{2}{3}.3+3=2+3=5.\)

c)

Từ kết quả câu a và câu b ta thấy:

Khi \(x\) lấy cùng một giá trị thì giá trị của \(g(x)\) lớn hơn giá trị của \(f(x)\) là \(3\) đơn vị.

(Chú ý: Hai hàm số \(y=\dfrac{2}{3} x\) và \(y = \dfrac{2}{3} x + 3\) đều là hàm số đồng biến vì khi \(x\) tăng thì \(y\) cũng nhận được các giá trị tương ứng tăng lên).

Bài 2 trang 45 SGK Toán lớp 9 tập 1

Câu hỏi:

Cho hàm số \(\displaystyle y =  - {1 \over 2}x + 3\)  

a) Tính các giá trị tương ứng của y theo các giá trị của x rồi điền vào bảng sau:

b) Hàm số đã cho là hàm số đồng biến hay nghịch biến ? Vì sao ?

Phương pháp:

a) Lần lượt thay từng giá trị của \(x\) vào công thức hàm số \(y=f(x)\) ta tính được giá trị \(y\) của hàm số tại điểm đó. 

b) Với \({x_1},{x_2} \in \mathbb{R}\):

Nếu \( x_1  < x_2\)  và   \(f(x_1) < f(x_2)\)  thì hàm số \(y=f(x)\) đồng biến trên \(\mathbb{R}\).

Nếu \( x_1  < x_2\)  và   \(f(x_1) > f(x_2)\)  thì hàm số \(y=f(x)\) nghịch biến trên \(\mathbb{R}\).

Lời giải:

a) Ta có \(y=f(x)=-\dfrac{1}{2}x+3\).

Với \(y =  - \dfrac{1}{2}x + 3\) thay các giá trị của \(x\) vào biểu thức của \(y\), ta được:

+) \(f\left( { - 2,5} \right) =  - \dfrac{1}{2}.\left( { - 2,5} \right) + 3 \)

\(=(-0,5).(-2,5)+3\)\(=1,25+3 = 4,25\)

+)  \(f\left( { - 2} \right) =  - \dfrac{1}{2}.\left( { - 2} \right) + 3 \)

 \(=(-0,5).(-2)+3=1+3 = 4\).

 +) \(f\left( { - 1,5} \right) = - \dfrac{1}{2}.\left( { - 1,5} \right) + 3 \)

\(= (-0,5).(-1,5)+3\)\(=0,75+3= 3,75\).

 +) \(f\left( { - 1} \right) = - \dfrac{1}{2}.\left( { - 1} \right) + 3 \)

\(= (-0,5).(-1)+3=0,5+3 = 3,5\).

+) \(f\left( { - 0,5} \right) =  - \dfrac{1}{2}.\left( { - 0,5} \right) + 3\)

\(= (-0,5).(-0,5)+3\)\(=0,25+3= 3,25\).

 +) \(f\left( 0 \right) =- \dfrac{1}{2}. 0 + 3\)\( = (-0,5).0+3=0+3= 3\)

 +) \(f\left( {0,5} \right) =  - \dfrac{1}{2}. 0,5 + 3\)

\(= (-0,5).0,5+3\)\(=-0,25+3= 2,75\)

 +) \(f\left( 1 \right) =  - \dfrac{1}{2}. 1 + 3 \)

\(= (-0,5).1+3=-0,5+3= 2,5\).

+) \(f\left( {1,5} \right) = - \dfrac{1}{2}.1,5 + 3 \)

\(=(-0,5).1,5+3=-0,75+3\)\( = 2,25\)

+)  \(f\left( 2 \right) =  - \dfrac{1}{2}. 2 + 3 \)

\(= (-0,5).2+3=-1+3= 2\).

 +) \(f\left( {2,5} \right) = - \dfrac{1}{2}.2,5 + 3 \)

\(= (-0,5).2,5+3=-1,25+3 \)\(= 1,75\)

Ta có bảng sau:

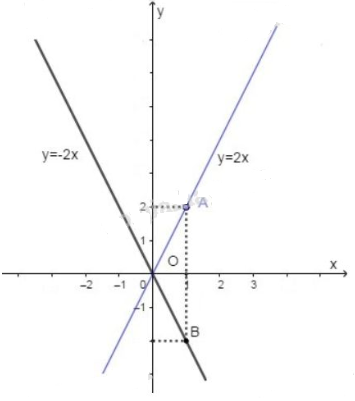
b)

Nhìn vào bảng giá trị của hàm số ở câu \(a\) ta thấy khi \(x\) càng tăng thì giá trị của \(f(x)\) càng giảm. Do đó hàm số nghịch biến trên \(\mathbb R\).

Bài 3 trang 45 SGK Toán lớp 9 tập 1

Câu hỏi:

Cho hai hàm số y = 2x và y = -2x. 

a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho.

b) Trong hai hàm số đã cho, hàm số nào đồng biến ? Hàm số nào nghịch biến ? Vì sao ?

Lời giải:

a)

+) Hàm số:  \(y = 2x\)

Cho \(x=0 \Rightarrow y=2.0=0 \Rightarrow O(0; 0) \).

Cho \(x=1 \Rightarrow y=2.1=2 \Rightarrow A(1; 2) \).

Đồ thị của hàm số \(y = 2x\) là đường thẳng đi qua \(O(0;0)\) và điểm \(A(1; 2)\).

+) Hàm số:  \(y = -2x\)

Cho \(x=0 \Rightarrow y=-2.0=0 \Rightarrow O(0; 0) \).

Cho \(x=1 \Rightarrow y=-2.1=-2 \Rightarrow B(1; -2) \).

Đồ thị của hàm số \(y = -2x\) là đường thẳng đi qua \(O(0;0)\) và điểm \(B(1; -2)\). 

b) Cách 1: Dùng định nghĩa

+) Xét hàm số: \(y=f(x)=2x\)

Với mọi \(x_1, x_2 \in \mathbb{R}\)

Giả sử \(x_1 < x_2 \Rightarrow 2x_1 < 2x_2 \Rightarrow f(x_1) < f(x_2)\)

Do đó hàm số \(y = 2x\) là hàm số đồng biến trên \(\mathbb R\). 

+) Xét hàm số \(y=g(x)=-2x\)

Với mọi \(x_1, x_2 \in \mathbb{R}\)

Giả sử  \(x_1 < x_2 \Rightarrow -2x_1 > -2x_2 \Rightarrow g(x_1) > g(x_2)\)

Do đó hàm số \(y = -2x\) là hàm số nghịch biến trên \(\mathbb R\).   

Cách 2:

Lập bảng giá trị cho \(x\) nhận các giá trị \(-2; -1; 0; 1; 2\) ta được bảng sau:

Quan sát bảng trên ta thấy: Khi \(x\) càng tăng thì giá trị của hàm số \(y=2x\) càng tăng và giá trị của hàm số \(y=-2x\) càng giảm. Do đó:

Hàm số \(y = -2x\) nghịch biến, hàm số \(y = 2x\) đồng biến.

Sachbaitap.com