Tải ngay
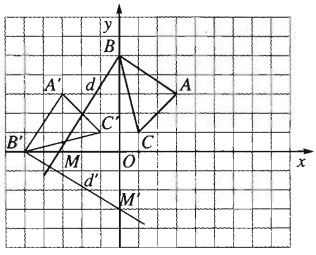
Bài 1.16 trang 26 Sách bài tập (SBT) Hình học 11Hãy xác định tọa độ các đỉnh của tam giác A’B’C’ và phương trình của đường thẳng d theo thứ tự là ảnh của tam giác ABC và đường thẳng d qua phép quay tâm O, góc quay 90°. Trong mặt phẳng Oxy cho các điểm A(3; 3), B(0; 5), C(1; 1) và đường thẳng d có phương trình \(5x - 3y + 15 = 0\). Hãy xác định tọa độ các đỉnh của tam giác A’B’C’ và phương trình của đường thẳng d theo thứ tự là ảnh của tam giác ABC và đường thẳng d qua phép quay tâm O, góc quay 90°. Giải:
Gọi \({Q_{\left( {0;90^\circ } \right)}}\) là phép quay tâm O, góc quay 90°. \(A'\left( { - 3;3} \right)\) \(B'\left( {5;0} \right)\) \(C'\left( { - 1;1} \right)\) d đi qua B và \(M\left( { - 3;0} \right)\) \(M' = {Q_{\left( {0;90^\circ } \right)}};M = \left( {0; - 3} \right)\) nên d' là đường thẳng B'M' có phương trình \(3x + 5y + 15 = 0\)
Xem lời giải SGK - Toán 11 - Xem ngay >> Học trực tuyến Lớp 11 cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng. Cam kết giúp học sinh lớp 11 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 5. Phép quay
|
-
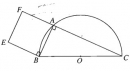
Bài 1.17 trang 27 Sách bài tập (SBT) Hình học 11
Cho nửa đường tròn tâm O đường kính BC. Điểm A chạy trên nửa đường tròn đó. Dựng về phía ngoài của tam giác ABC hình vuông ABEF. Chứng minh rằng E chạy trên một nửa đường tròn cố định.
-
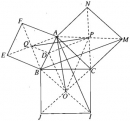
Bài 1.18 trang 27 Sách bài tập (SBT) Hình học 11
Cho tam giác ABC. Dựng về phía ngoài của tam giác các hình vuông BCIJ, ACMN, ABEF và gọi O, P, Q lần lượt là tâm đối xứng của chúng
-
Bài 1.19 trang 30 Sách bài tập (SBT) Hình học 11
Tìm tọa độ của điểm M’ là ảnh của điểm M qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng qua trục Oy
-
Bài 1.20 trang 30 Sách bài tập (SBT) Hình học 11
Tìm ảnh của d qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc 90°
