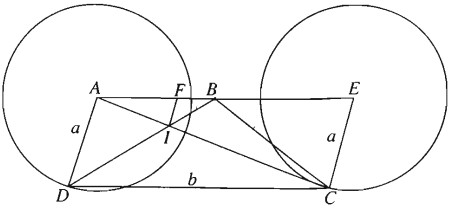
Bài 1.30 trang 39 Sách bài tập (SBT) Hình học 11Cho hình thang ABCD có AB song song với CD, AD = a, DC = b còn hai đỉnh A, B cố định. Gọi I là giao điểm của hai đường chéo. Cho hình thang ABCD có AB song song với CD, AD = a, DC = b còn hai đỉnh A, B cố định. Gọi I là giao điểm của hai đường chéo. a) Tìm tập hợp các điểm C khi D thay đổi b) Tìm tập hợp các điểm I khi C và D thay đổi như trong câu a) . Giải:
a) Dựng hình bình hành ADCE. Ta có \(\overrightarrow {DC} = \overrightarrow {A{\rm{E}}}\) không đổi. Do AE = b không đổi, nên E cố định. Do \(A{\rm{D}} = EC = a\) nên khi D chạy trên đường tròn \(\left( {A;a} \right)\) thì C chạy trên đường tròn \(\left( {E;a} \right)\) là ảnh của \(\left( {A;a} \right)\) qua phép tịnh tiến theo \(\overrightarrow {A{\rm{E}}} \). b) Đường thẳng qua I, song song với AD cắt AE tại F. Ta có \(\eqalign{ Do đó có thể xem I là ảnh của C qua phép vị tự tâm A, tỉ số \({{AB} \over {AB + b}}\). Vậy khi C chạy trên (E;a) thì I chạy trên đường tròn là ảnh của (E;a) qua phép vị tự nói trên.
Xem lời giải SGK - Toán 11 - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 8. Phép đồng dạng
|
-
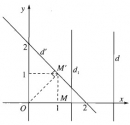
Bài 1.27 trang 38 Sách bài tập (SBT) Hình học 11
Hãy viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O
-

Bài 1.28 trang 38 Sách bài tập (SBT) Hình học 11
Hãy viết phương trình đường tròn (C’) là ảnh của (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = -2 và phép đối xứng qua trục Ox
-

Bài 1.29 trang 38 Sách bài tập (SBT) Hình học 11
Chứng minh rằng hai đa giác đều có cùng số cạnh luôn đồng dạng với nhau
-

Bài 1.31 trang 39 Sách bài tập (SBT) Hình học 11
Hãy viết phương trình đường thẳng d’ là ảnh của d qua phép tịnh tiến theo vectơ

 Tải ngay
Tải ngay