Tải ngay
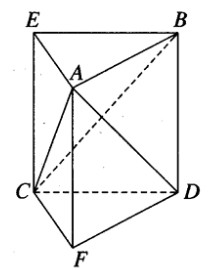
Bài 1.34 trang 22 sách bài tập (SBT) – Hình học 12Cho hai đoạn thẳng AB và CD chéo nhau, AC là đường vuông góc chung của chúng. Biết rằng AC = h, AB = a, CD = b và góc giữa hai đường thẳng AB và CD bằng 600. Hãy tính thể tích của khối tứ diện ABCD. Cho hai đoạn thẳng AB và CD chéo nhau, AC là đường vuông góc chung của chúng. Biết rằng AC = h, AB = a, CD = b và góc giữa hai đường thẳng AB và CD bằng 600. Hãy tính thể tích của khối tứ diện ABCD. Hướng dẫn làm bài:
Dựng BE song song và bằng DC, DF song song và bằng BA. Khi đó, ABE.FDC là một lăng trụ đứng. Ta có: \({S_{ABE}} = {1 \over 2}ab.\sin {60^0} = ab{{\sqrt 3 } \over 4}\) , \({V_{C.ABE}} = {1 \over 3}.{{\sqrt 3 } \over 4}ab.h = {{\sqrt 3 } \over {12}}abh\) Từ đó suy ra \({V_{A.BCD}} = {V_{A.BCE}} = {{\sqrt 3 } \over {12}}abh\) Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
ĐỀ TOÁN TỔNG HỢP - CHƯƠNG I. KHỐI ĐA ĐIẾN
|
-
Bài 1.35 trang 22 sách bài tập (SBT) – Hình học 12
Cho tứ diện đều ABCD. Gọi (H) là hình bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện đều đó. Tính tỉ số .
-
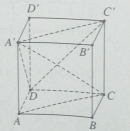
Bài 1.36 trang 23 sách bài tập (SBT) – Hình học 12
Cho hình lập phương ABCD.A’B’C’D’ cạnh a, M là trung điểm của BB’ Tính theo a :
-
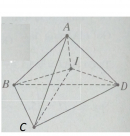
Bài 1.37 trang 23 sách bài tập (SBT) – Hình học 12
Cho tứ diện ABCD. Gọi hA , hB, hC, hD lần lượt là các đường cao của tứ diện xuất phát từ A, B, C, D và r là bán kính mặt cầu nội tiếp tứ diện. Chứng minh rằng:
-
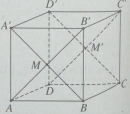
Đề 1 trang 23 Sách bài tập (SBT) Hình học 12
Cho hình lập phương ABCD. A’B’C’D’. Chứng minh hai tứ diện ABCB’ và AA’D’B’ bằng nhau.
