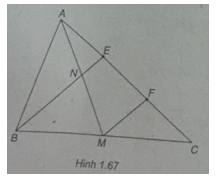
Bài 1.54 trang 45 Sách bài tập (SBT) Toán Hình học 10

Bình chọn:

4 trên 2 phiếu

Cho tam giác ABC có trung tuyến AM. Trên cạnh AC lấy hai điểm E và F sao cho

Cho tam giác ABC có trung tuyến AM. Trên cạnh AC lấy hai điểm E và F sao cho AE = EF = FC. BE cắt trung tuyến AM tại N. Tính \(\overrightarrow {AE} + \overrightarrow {AF} + \overrightarrow {AN} + \overrightarrow {MN} \)

Gợi ý làm bài

(h.1.67)

Ta có \(\overrightarrow {AE} = \overrightarrow {FC} \)

Vì MF // BE nên N là trung điểm của AM, suy ra \(\overrightarrow {AN} + \overrightarrow {MN} = \overrightarrow 0 \)

Do đó \(\overrightarrow {AE} + \overrightarrow {AF} + \overrightarrow {AN} + \overrightarrow {MN} = \overrightarrow {AF} + \overrightarrow {FC} = \overrightarrow {AC}\)

Sachbaitap.net

Báo lỗi - Góp ý

Xem lời giải SGK - Toán 10 - Xem ngay

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, hoàn trả học phí nếu học không hiệu quả.