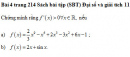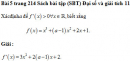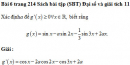Bài 2 trang 214 Sách bài tập (SBT) Đại số và giải tích 11Giải phương trình Giải phương trình \(f'\left( x \right) = g\left( x \right),\) biết rằng a) \(f\left( x \right) = {{1 - \cos 3x} \over 3};g\left( x \right) = \left( {\cos 6x - 1} \right)\cot 3x.\) b) \(f\left( x \right) = {1 \over 2}\cos 2x;g\left( x \right) = 1 - {\left( {\cos 3x + \sin 3x} \right)^2}.\) c) \(f\left( x \right) = {1 \over 2}\sin 2x + 5\cos x;g\left( x \right) = 3{\sin ^2}x + {3 \over {1 + {{\tan }^2}x}}.\) Giải : a) \(f\left( x \right) = {{1 - \cos 3x} \over 3} \Rightarrow f'\left( x \right) = \sin 3x.\) Ta có \(f'\left( x \right) = g\left( x \right) \Leftrightarrow \left( {\cos 6x - 1} \right).\cot 3x = \sin 3x\) (điều kiện: \(\sin 3x \ne 0 \Leftrightarrow \cos 3x \ne \pm 1\) ) \(\eqalign{ b) \(f\left( x \right) = {1 \over 2}\cos 2x \Rightarrow f'\left( x \right) = - \sin 2x.\) Ta có \(\eqalign{ c) \(f\left( x \right) = {1 \over 2}\sin 2x + 5\cos x \Rightarrow f'\left( x \right) = \cos 2x - 5\sin x.\) Ta có \(\eqalign{ Đặt \(t = \sin x,t \in \left[ { - 1;1} \right],\) ta có phương trình \(2{t^2} + 5t + 2 = 0.\) Giải phương trình \(t = - {1 \over 2}\) ta được (loại t = -2 ). \(\eqalign{
Xem lời giải SGK - Toán 11 - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Ôn tập Chương V - Đạo hàm
|
-

Bài 3 trang 214 Sách bài tập (SBT) Đại số và giải tích 11
Tìm đạo hàm của hàm số tại điểm đã chỉ ra :

 Tải ngay
Tải ngay