Bài 2.10 trang 164 Sách bài tập (SBT) Đại số và giải tích 11Chứng minh rằng Cho khoảng \(K,{x_0} \in K\) và hàm số \(y = f\left( x \right)\) xác định trên \(K\backslash \left\{ {{x_0}} \right\}\) Chứng minh rằng nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = + \infty \) thì luôn tồn tại ít nhất một số c thuộc \(K\backslash \left\{ {{x_0}} \right\}\) sao cho \(f\left( c \right) > 0\) Giải: Vì \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = + \infty \) nên với dãy số \(\left( {{x_n}} \right)\) bất kì, \({x_n} \in K\backslash \left\{ {{x_0}} \right\}\) và \({x_n} \to {x_0}\) ta luôn có \(\mathop {\lim }\limits_{n \to + \infty } f\left( {{x_n}} \right) = + \infty \) Từ định nghĩa suy ra \(f\left( {{x_n}} \right)\) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi. Nếu số dương này là 1 thì \(f\left( {{x_n}} \right) > 1\) kể từ một số hạng nàođó trởđi. Nói cách khác, luôn tồn tạiít nhất một số \({x_k} \in K\backslash \left\{ {{x_o}} \right\}\) sao cho \(f\left( {{x_k}} \right) > 1\). Đặt \(c = {x_k}\) ta có \(f\left( c \right) > 0\)
Xem lời giải SGK - Toán 11 - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 2. Giới hạn của hàm số
|
-

Bài 2.11 trang 165 Sách bài tập (SBT) Đại số và giải tích 11
Cho hàm số y = f(x) xác định trên khoảng:
-
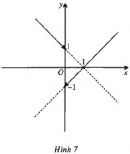
Bài 3.1 trang 168 Sách bài tập (SBT) Đại số và giải tích 11
Vẽ đồ thị của hàm số này.Từ đồ thị dự đoán các khoảng trên đó hàm số liên tục và chứng minh dự đoán đó.
-

Bài 3.2 trang 168 Sách bài tập (SBT) Đại số và giải tích 11
Cho ví dụ về một hàm số liên tục trên (a; b]
-

Bài 3.3 trang 169 Sách bài tập (SBT) Đại số và giải tích 11
Chứng minh rằng nếu một hàm số liên tục trên (a; b] và trên [b; c) thì nó liên tục trên (a; c)

 Tải ngay
Tải ngay







