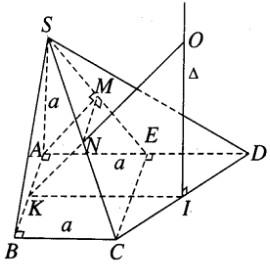
Bài 2.21 trang 64 sách bài tập (SBT) – Hình học 12Hình chóp S.ABCD có SA = a là chiều cao của hình chóp và đáy ABCD là hình thang vuông tại A và B có AB = BC = a và AD = 2a. Gọi E là trung điểm của cạnh AD. Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.CDE Hình chóp S.ABCD có SA = a là chiều cao của hình chóp và đáy ABCD là hình thang vuông tại A và B có AB = BC = a và AD = 2a. Gọi E là trung điểm của cạnh AD. Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.CDE Hướng dẫn làm bài:
Tam giác CED là tam giác vuông cân tại E nên trục của đường tròn đi qua ba điểm C, E, D là đường thẳng \(\Delta \) đi qua trung điểm I của đoạn thẳng CD và song song với SA. Gọi M, N lần lượt là trung điểm của SE và SC. Ta có mặt phẳng (ABNM) là mặt phẳng trung trực của đoạn SE. Vậy tâm O của mặt cầu ngoại tiếp hình chóp S.CDE chính là giao điểm của \(\Delta \) và mp(ABNM). Gọi K là trung điểm của AB thì KN // AM và do đó KN //(SAE). Ta có IK // AD nên IK // (SAE). Vậy KN và \(\Delta \) đồng phẳng và ta có O là giao điểm cần tìm. Chú ý rằng OIK là tam giác vuông cân, vì \(\widehat {OKI} = \widehat {MAE} = {45^0}\) Ta có OI = IK, trong đó \(IK = {{BC + AD} \over 2} = {{a + 2a} \over 2} = {{3a} \over 2}\) Vậy \(O{C^2} = O{I^2} + I{C^2} = {{9{a^2}} \over 4} + {{2{a^2}} \over 4}\) (vì \(CD = a\sqrt 2 ;IC = {{CD} \over 2}\)). Do đó, bán kính mặt cầu ngoại tiếp hình chóp S.CDE là: \(r = OC = {{a\sqrt {11} } \over 2}\). Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 2. Mặt cầu
|
-
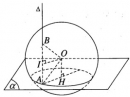
Bài 2.22 trang 64 sách bài tập (SBT) – Hình học 12
Cho hình cầu tâm O bán kính r. Lấy một điểm A trên mặt cầu và gọi là mặt phẳng đi qua A sao cho góc giữa OA và bằng 300.
-
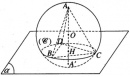
Bài 2.23 trang 64 sách bài tập (SBT) – Hình học 12
Cho hình cầu đường kính AA’ = 2r. Gọi H là một điểm trên đoạn AA’ sao cho . Mặt phẳng qua H và vuông góc với AA’ cắt hình cầu theo đường tròn (C).
-
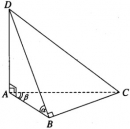
Bài 2.24 trang 65 sách bài tập (SBT) – Hình học 12
Cho tứ diện ABCD có và . Khi quay tất cả các cạnh của tứ diện đó quanh cạnh AB có những hình nón nào được tạo thành ? Hãy kể tên các hình nón đó.
-
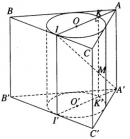
Bài 2.25 trang 65 sách bài tập (SBT) – Hình học 12
Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và có đường cao h.

 Tải ngay
Tải ngay