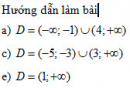Bài 2.22 trang 116 Sách bài tập (SBT) Giải tích 12Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = {2^{|x|}}\) trên đoạn [-1; 1]. Hướng dẫn làm bài: Trên đoạn [-1; 1], ta có : \(\begin{array}{l} Do đó, trên đoạn [0; 1] hàm số đồng biến, trên đoạn [-1; 0] hàm số nghịch biến. Suy ra các giá trị lớn nhất và giá trị nhỏ nhất sẽ đạt được tại các đầu mút. Ta có: \(y( - 1) = {2^{ - ( - 1)}} = {2^1} = 2,y(0) = {2^0} = 1,y(1) = {2^1} = 2\) Vậy \(\mathop {M{\rm{ax}}}\limits_{{\rm{[}} - 1;1]} y = y(1) = y( - 1) = 2,\mathop {\min }\limits_{{\rm{[}} - 1;1]} y = y(0) = 1\). Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 4. Hàm số mũ. Hàm số logarit
|
-
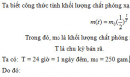
Bài 2.23 trang 116 Sách bài tập (SBT) Giải tích 12
Cho biết chu kỳ bán rã của một chất phóng xạ là 24 giờ (1 ngày đêm). Hỏi 250 gam chất đó sẽ còn lại bao nhiêu gam sau:
-
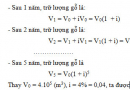
Bài 2.24 trang 116 Sách bài tập (SBT) Giải tích 12
Một khu rừng có trữ lượng gỗ 4.105 mét khối. Biết tốc độ sinh trưởng của các cây ở khu rừng đó là 4% mỗi năm. Hỏi sau 5 năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ?
-
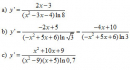
Bài 2.26 trang 116 Sách bài tập (SBT) Giải tích 12
Tình đạo hàm của các hàm số đã cho ở bài tập 2.25.

 Tải ngay
Tải ngay