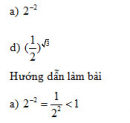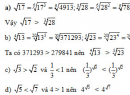Bài 2.3 trang 95 Sách bài tập (SBT) Giải tích 12Cho a và b là các số dương. Đơn giản các biểu thức sau: Cho a và b là các số dương. Đơn giản các biểu thức sau: a) \({{{a^{{4 \over 3}}}({a^{ - {1 \over 3}}} + {a^{{2 \over 3}}})} \over {{a^{{1 \over 4}}}({a^{{3 \over 4}}} + {a^{ - {1 \over 4}}})}}\) b) \({{{a^{{1 \over 3}}}\sqrt b + {b^{{1 \over 3}}}\sqrt a } \over {\root 6 \of a + \root 6 \of b }}\) c) \((\root 3 \of a + \root 3 \of b )({a^{{2 \over 3}}} + {b^{{2 \over 3}}} - \root 3 \of {ab} )\) d) \(({a^{{1 \over 3}}} + {b^{{1 \over 3}}}):(2 + \root 3 \of {{a \over b}} + \root 3 \of {{b \over a}} )\) Hướng dẫn làm bài: Với a và b là các số dương ta có: a) \({{{a^{{4 \over 3}}}({a^{ - {1 \over 3}}} + {a^{{2 \over 3}}})} \over {{a^{{1 \over 4}}}({a^{{3 \over 4}}} + {a^{ - {1 \over 4}}})}} = {{a + {a^2}} \over {a + 1}} = {{a(a + 1)} \over {a + 1}} = a\) b) \({{{a^{{1 \over 3}}}\sqrt b + {b^{{1 \over 3}}}\sqrt a } \over {\root 6 \of a + \root 6 \of b }} = {{{a^{{1 \over 3}}}{b^{{1 \over 2}}} + {b^{{1 \over 3}}}{a^{{1 \over 2}}}} \over {{a^{{1 \over 6}}} + {b^{{1 \over 6}}}}}\) \(= {{{a^{{1 \over 3}}}{b^{{1 \over 3}}}({b^{{1 \over 2} - {1 \over 3}}} + {a^{{1 \over 2} - {1 \over 3}}})} \over {{a^{{1 \over 6}}} + {b^{{1 \over 6}}}}} = {{{a^{{1 \over 3}}}{b^{{1 \over 3}}}({b^{{1 \over 6}}} + {a^{{1 \over 6}}})} \over {{a^{{1 \over 6}}} + {b^{{1 \over 6}}}}} = \root 3 \of {ab} \) c) \((\root 3 \of a + \root 3 \of b )({a^{{2 \over 3}}} + {b^{{2 \over 3}}} - \root 3 \of {ab} )\) \(= ({a^{{1 \over 3}}} + {b^{{1 \over 3}}})({a^{{2 \over 3}}} - {a^{{1 \over 3}}}{b^{{1 \over 3}}} + {b^{{2 \over 3}}})\) \(= {({a^{{1 \over 3}}})^3} + {({b^{{1 \over 3}}})^3} = a + b\) d) \(({a^{{1 \over 3}}} + {b^{{1 \over 3}}}):(2 + \root 3 \of {{a \over b}} + \root 3 \of {{b \over a}} )\) \(= {{{a^{{1 \over 3}}} + {b^{{1 \over 3}}}} \over {{{2\root 3 \of {ab} + \root 3 \of {{a^2}} + \root 3 \of {{b^2}} } \over {\root 3 \of {ab} }}}} = {{(\root 3 \of a + \root 3 \of b )\root 3 \of {ab} } \over {{{(\root 3 \of a + \root 3 \of b )}^2}}} = {{\root 3 \of {ab} } \over {\root 3 \of a + \root 3 \of b }}\) Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 1. Lũy thừa
|

 Tải ngay
Tải ngay