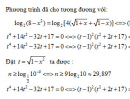Bài 2.34 trang 125 Sách bài tập (SBT) Giải tích 12Giải các phương trình sau bằng phương pháp đồ thị: Giải các phương trình sau bằng phương pháp đồ thị: a) \({\log _{\frac{1}{3}}}x = 3x\) b) \({\log _3}x = - x + 11\) c) \({\log _4}x = \frac{4}{x}\) d) \({16^x} = {\log _{\frac{1}{2}}}x\) Hướng dẫn làm bài: a) Vẽ đồ thị của hàm số \({\log _{\frac{1}{3}}}x = 3x\) và đường thẳng y = 3x trên cùng một hệ trục tọa độ (H.61), ta thấy chúng cắt nhau tại điểm có hoành độ \(x = \frac{1}{3}\) Thử lại, ta thấy giá trị này thỏa mãn phương trình đã cho. Mặt khác, hàm số \(y = {\log _{\frac{1}{3}}}x\) luôn nghịch biến, hàm số y = 3x luôn đồng biến. Vậy \(x = \frac{1}{3}\) là nghiệm duy nhất của phương trình đã cho. b) Vẽ đồ thị của hàm số \(y = {\log _3}x\) và đường thẳng y = - x + 11 trên cùng một hệ trục tọa độ (H.62) , ta thấy chúng cắt nhau tại điểm có hoành độ x = 9. Lập luận tương tự câu a), ta cũng có đây là nghiệm duy nhất của phương trình đã cho. c) Vẽ đồ thị của các hàm số \(y = {\log _4}x\) và \(y = \frac{4}{x}\) trên cùng một hệ trục tọa độ (H.63), ta thấy chúng cắt nhau tại điểm có hoành độ x = 4. Ta cũng có hàm số \(y = {\log _3}x\) luôn đồng biến, hàm số \(y = \frac{4}{x}\) luôn nghịch biến trên \((0; + \infty )\) . Do đó, x = 4 là nghiệm duy nhất.
d) Vẽ đồ thị của các hàm số \(y = {16^x}\) và \(y = {\log _{\frac{1}{2}}}x\) trên cùng một hệ trục tọa độ (H.64), ta thấy chúng cắt nhau tại điểm có hoành độ \(x = \frac{1}{4}\) . Thử lại, ta thấy \(x = \frac{1}{4}\) thỏa mãn phương trình đã cho. Mặt khác, hàm số luôn đồng biến, hàm số luôn nghịch biến. Vậy \(x = \frac{1}{4}\) là nghiệm duy nhất của phương trình. Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 5. Phương trình mũ và phương trình logarit
|

 Tải ngay
Tải ngay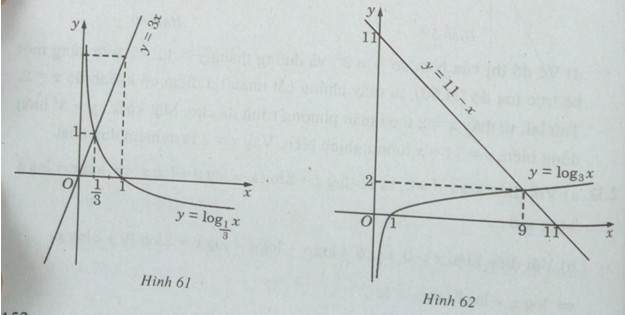
 6
6