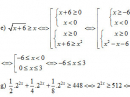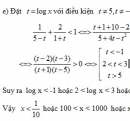Bài 2.38 trang 126 Sách bài tập (SBT) Giải tích 12

Bình chọn:

4 trên 2 phiếu

Giải phương trình:

\(f(x) = 2\sqrt {x + 2} - {x^3} + 4{\log _2}(8 - {x^2}) + {\log _{\frac{1}{2}}}(\sqrt {1 + x} + \sqrt {1 - x} ) - 2 = 0\)

(Đề thi Đại học năm 2011, khối D)

Hướng dẫn làm bài:

Điều kiện: \( - 1 \le x \le 1\)

Phương trình đã cho tương đương với:

\(\eqalign{
& {\log _2}(8 - {x^2}) = {\log _2}{\rm{[}}4(\sqrt {1 + x} + \sqrt {1 - x} ){\rm{]}} \cr
& \Leftrightarrow {(8 - {x^2})^2} = 16(2 + 2\sqrt {1 - {x^2}} ) \cr} \)

Đặt \(t = \sqrt {1 - {x^2}} \) ta được :

\(\eqalign{
& {t^4} + 14{t^2} - 32t + 17 = 0 \cr
& \Leftrightarrow {(t - 1)^2}({t^2} + 2t + 17) = 0 \cr
& \Leftrightarrow t = 1 \cr} \)

Suy ra x = 0. Vậy phương trình có nghiệm x = 0

Sachbaitap.com

Báo lỗi - Góp ý

Xem lời giải SGK - Toán 12 - Xem ngay

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.