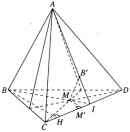
Bài 2.36 trang 83 Sách bài tập (SBT) Hình học 11Hãy chọn phép chiếu song song với phương chiếu của và mặt phẳng chiếu thích hợp để hình chiếu song song của một tứ diện cho trước là một hình bình hành. Hãy chọn phép chiếu song song với phương chiếu của và mặt phẳng chiếu thích hợp để hình chiếu song song của một tứ diện cho trước là một hình bình hành. Giải:
Cho tứ diện ABCD. Gọi d là một đường thẳng không song song với với các cạnh của tứ diện và \(\left( \alpha \right)\) là một mặt phảng cắt d. Gọi A’, B’, C’, D’ lần lượt là hình chiếu của A, B, C, D trên mặt phẳng \(\left( \alpha \right)\). Gọi P và Q lần lượt là trung điểm của hai cạnh đối diện AB và CD. Khi đó hình chiếu của P’ và Q’ của P và Q sẽ lần lượt là trung điểm của A’B’ và C’D’. Muốn cho A’, B’, C’, D’ là các đỉnh của một hình bình hành ta chỉ cần chọn phương chiếu d sao cho d song song với đường thẳng PQ. Vậy để hình chiếu song song của một tứ diện là một hình bình hành ta có thể chọn : - Phương chiếu d là phương của một trong ba đường thẳng đi qua trung điểm của hai cạnh đối diện của tứ diện cho trước. - Mặt phẳng chiếu \(\left( \alpha \right)\) là mặt phẳng tùy ý, nhưng phải cắt đường thẳng d. Sachbaitap.com
Xem lời giải SGK - Toán 11 - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 5. Phép chiếu song song. Hình biểu diễn của một hình không gian
|
-
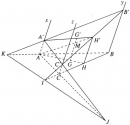
Bài 2.37 trang 84 Sách bài tập (SBT) Hình học 11
Trên Ax lấy đoạn AA’ = a, trên By lấy đoạn BB’ = b, trên Cz lấy đoạn CC’ = c.
-
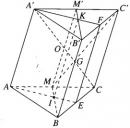
Bài 2.39 trang 84 Sách bài tập (SBT) Hình học 11
Từ các đỉnh của tam giác ABC ta kẻ các đoạn thẳng AA’, BB’, CC’ song song cùng chiều, bằng nhau và không nằm trong mặt phẳng của tam giác. Gọi I, G và K lần lượt là trọng tâm của các tam giác ABC, ACC’, A’B’C’.
-
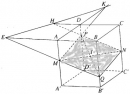
Bài 2.40 trang 84 Sách bài tập (SBT) Hình học 11
Cho hình hộp ABCD.A’B’C’D’. Gọi M và N lần lượt là trung điểm của hai cạnh bên AA’ và CC’. Một điểm P nằm trên cạnh bên DD’.

 Tải ngay
Tải ngay