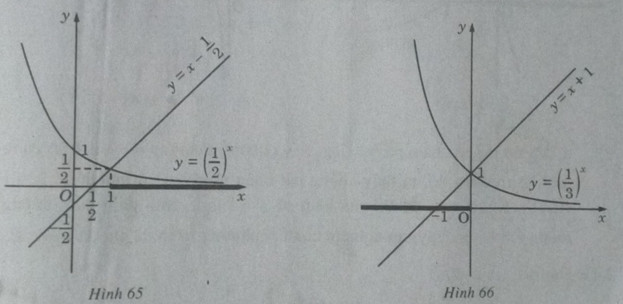
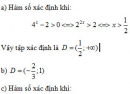Bài 2.41 trang 132 Sách bài tập (SBT) Giải tích 12Giải các bất phương trình sau bằng đồ thị: Giải các bất phương trình sau bằng đồ thị: a) \({(\frac{1}{2})^x} < x - \frac{1}{2}\) b) \({(\frac{1}{3})^x} \ge x + 1\) c) \({\log _{\frac{1}{3}}}x > 3x\) d) \({\log _2}x \le 6 - x\) Hướng dẫn làm bài: a) Vẽ đồ thị của hàm số \(y = {(\frac{1}{2})^x}\) và đường thẳng \(y = x - \frac{1}{2}\) trên cùng một hệ trục tọa độ (H.65), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Với x > 1 đồ thị của hàm số \(y = {(\frac{1}{2})^x}\) nằm phía dưới đường thẳng \(y = x - \frac{1}{2}\) . Vậy tập nghiệm của bất phương trình đã cho là \((1; + \infty )\)
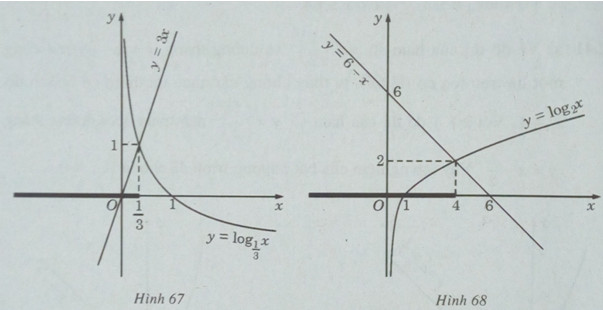
b) Vẽ đồ thị của hàm số \(y = {(\frac{1}{3})^x}\) và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.66), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0. Khi x < 0 đồ thị của hàm số \(y = {(\frac{1}{3})^x}\) nằm phía trên đường thẳng y = x + 1. Vậy tập nghiệm của bất phương trình đã cho là \(( - \infty ;0]\) c) Vẽ đồ thị của hàm số \(y = {\log _{\frac{1}{3}}}x\) và đường thẳng y = 3x trên cùng một hệ trục tọa độ ta thấy chúng cắt nhau tại điểm có hoành độ \(x = \frac{1}{3}\) (H.67) Khi \(x < \frac{1}{3}\) đồ thị của hàm số \(y = {\log _{\frac{1}{3}}}x\) nằm phía trên đường thẳng y = 3x. Vậy tập nghiệm của bất phương trình đã cho là \(( - \infty ;\frac{1}{3})\) . d) Vẽ đồ thị của hàm số \(y = {\log _2}x\) và đường thẳng y = 6 – x trên cùng một hệ trục tọa độ, ta thấy chúng cắt nhau tại điểm có hoành độ x = 4 (H.68). Khi x < 4, đồ thị của hàm số \(y = {\log _2}x\) nằm phía dưới y = 6 – x . Vậy tập nghiệm của bất phương trình đã cho là \(( - \infty ;4]\). Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 6. Bất phương trình mũ và bất phương trình logarit
|
-
Bài 2.43 trang 132 Sách bài tập (SBT) Giải tích 12
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
-
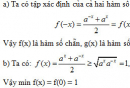
Bài 2.45 trang 133 Sách bài tập (SBT) Giải tích 12
Chứng minh rằng f(x) là hàm số chẵn, g(x) là hàm số lẻ.

 Tải ngay
Tải ngay