Tải ngay
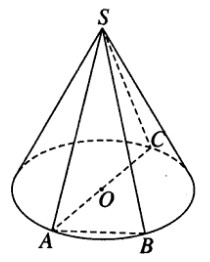
Bài 2.5 trang 50 sách bài tập (SBT) – Hình học 12.Chứng minh rằng trong một khối nón tròn xoay, góc ở đỉnh là góc lớn nhất trong số các góc được tạo nên bởi hai đường sinh của khối nón đó. Chứng minh rằng trong một khối nón tròn xoay, góc ở đỉnh là góc lớn nhất trong số các góc được tạo nên bởi hai đường sinh của khối nón đó. Hướng dẫn làm bài:
Xét hai đường sinh SA , SB tùy ý của hình nón. Vẽ đường kính AC của đường tròn đáy. Ta có góc ASC là góc ở đỉnh của hình nón. Hai tam giác ASC và ASB có hai cặp cạnh bằng nhau vì chúng cùng là đường sinh của hình nón. Ta có cạnh \(AC \ge AB\) nên \(\widehat {{\rm{AS}}C} \ge \widehat {ASB}\) . Đó là điều cần chứng minh. Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 1. Khái niệm về mặt tròn xoay
|
-
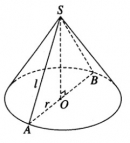
Bài 2.6 trang 50 sách bài tập (SBT) – Hình học 12.
Cho khối nón có bán kính đáy r = 12 cm và có góc ở đỉnh là . Hãy tính diện tích của thiết diện đi qua hai đường sinh vuông góc với nhau.
-
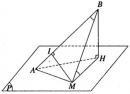
Bài 2.7 trang 50 sách bài tập (SBT) – Hình học 12.
Cho mặt phẳng (P). Gọi A là một điểm nằm trên (P) và B là một điểm nằm ngoài (P) sao cho hình chiếu H của B trên (P) không trùng với A.
-
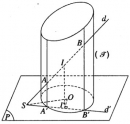
Bài 2.8 trang 50 sách bài tập (SBT) – Hình học 12.
Cho mặt trụ xoay và một điểm S cố định nằm ngoài . Một đường thẳng d thay đổi luôn luôn đi qua S cắt tại A và B. Chứng minh rằng trung điểm I của đoạn thẳng AB luôn luôn nằm trên một mặt trụ xác định.
-
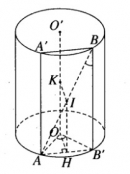
Bài 2.9 trang 50 sách bài tập (SBT) – Hình học 12.
Một khối trụ có bán kính đáy bằng r và chiều cao bằng .
