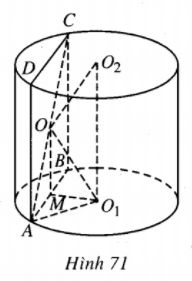
Bài 27 trang 59 Sách bài tập Hình học lớp 12 Nâng cao

Bình chọn:

4.9 trên 7 phiếu

Cho hình trụ có trục

Cho hình trụ có trục \({O_1}{O_2}\). Một mặt phẳng \(\left( \alpha \right)\) song song với trục \({O_1}{O_2}\), cắt hình trụ theo thiết diện là hình chữ nhật ABCD. Gọi O là tâm của thiết diện đó. Tính \(\widehat {{O_1}{\rm{O}}{{\rm{O}}_2}}\) biết rằng bán kính đường tròn ngoại tiếp hình chữ nhật ABCD bằng bán kính đường tròn đáy hình trụ.

Giải

Vì ABCD là hình chữ nhật nên O là trung điểm của AC.

Gọi M là trung điểm của AB thì \({O_1}M \bot AB,OM \bot AB\) và theo giải thiết, AO=AO₁.

Hai tam giác vuông MAO và MAO₁ có MA chung, \(OA = {O_1}A\) nên \(OM = {O_1}M.\)

Từ đó \(\widehat {{\rm{O}}{{\rm{O}}_1}M}\)= 45⁰, do đó \(\widehat {{\rm{O}}{{\rm{O}}_1}O_2}\) = 45⁰.

Dễ thấy \(\Delta {O_1}O{O_2}\) cân tại O, vậy \(\widehat {{O_1}{\rm{O}}{{\rm{O}}_2}}\) = 90⁰.

Sachbaitap.com

Báo lỗi - Góp ý

Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.