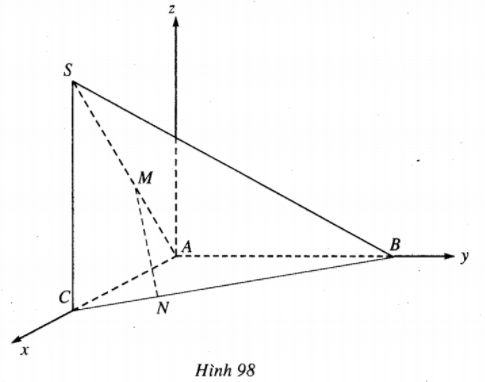
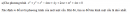Bài 28 trang 120 Sách bài tập Hình học lớp 12 Nâng caoCho tứ diện SABC Cho tứ diện SABC có \(SC = CA = AB = a\sqrt 2 ,SC \bot \left( {ABC} \right)\), tam giác ABC vuông tại A. Các điểm \(M \in SA,N \in BC\) sao cho \(AM = CN = t(0 < t < 2a)\) a) Tính độ dài đoạn MN. Tìm giá trị t để MN ngắn nhất. b) Khi đoạn MN ngắn nhất, chứng minh MN là đường vuông góc chung của BC và SA. Giải a) Ta chọn hệ trục Oxyz sao cho gốc tọa độ O trùng A, tia Ox chứa AC, tia Oy chứa AB và tia Oz cùng hướng tới tia CS (h.98). Khi đó, ta có: \(A(0;0;0),B(0;a\sqrt 2 ;0),C(a\sqrt 2 ;0;0),\) \(S(a\sqrt 2 ;0;a\sqrt 2 ),\)
\(\eqalign{ & M\left( {{{t\sqrt 2 } \over 2};0;{{t\sqrt 2 } \over 2}} \right);N\left( {a\sqrt 2 - {{t\sqrt 2 } \over 2};{{t\sqrt 2 } \over 2};0} \right) \cr & \Rightarrow \overrightarrow {MN} = \left( {\sqrt 2 (a - t);{{t\sqrt 2 } \over 2}; - {{t\sqrt 2 } \over 2}} \right) \cr & \Rightarrow {MN} = \sqrt {2({a^2} - 2at + {t^2}) + {{{t^2}} \over 2} + {{{t^2}} \over 2}} \cr&\;\;\;\;\;\;\;\;\;\;\;\;\;= \sqrt {3{t^2} - 4at + 2{a^2}} \cr & \;\;\;\;\;\;\;\;\;\;\;\;\;= \sqrt {3{{\left( {t - {{2a} \over 3}} \right)}^2} + {{2{a^2}} \over 3}} \ge {{a\sqrt 6 } \over 3}. \cr} \) Dấu "=" xảy ra khi \(t = {{2a} \over 3}\) thỏa mãn điều kiện 0 < t < 2a. Vậy MN ngắn nhất bằng \({{a\sqrt 6 } \over 3}\) khi \(t = {{2a} \over 3}.\) b) Khi MN ngắn nhất thì : \(\overrightarrow {MN} = \left( {{{a\sqrt 2 } \over 3};{{a\sqrt 2 } \over 3}; - {{a\sqrt 2 } \over 3}} \right) \Rightarrow \left\{ \matrix{ \overrightarrow {MN} .\overrightarrow {SA} = 0 \hfill \cr \overrightarrow {MN} .\overrightarrow {BC} = 0 \hfill \cr} \right.\) \( \Rightarrow MN\) là đường vuông góc chung của SA và BC. Sachbaitap.com
Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 1. Hệ tọa độ trong không gian
|
-

Bài 33 trang 121 Sách bài tập Hình học lớp 12 Nâng cao
a)Tìm tập hợp tâm các mặt cầu đi qua điểm A(a;b;c) cho

 Tải ngay
Tải ngay