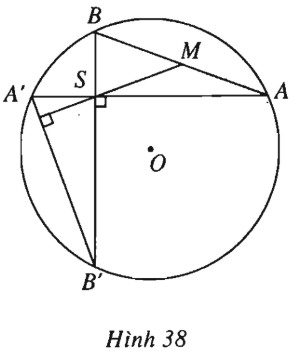
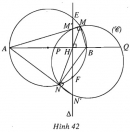
Bài 32 trang 43 SBT Hình học 10 Nâng caoGiải bài tập Bài 32 trang 43 SBT Hình học 10 Nâng cao Trong đường tròn \(C(O ; R)\) cho hai dây cung \(AA’, BB’\) vuông góc với nhau ở điểm \(S\) và gọi \(M\) là trung điểm của \(AB\). Chứng minh rằng \(SM \bot A'B'\). Giải (h.38).
Xét tích vô hướng \(\begin{array}{l}\overrightarrow {SM} .\overrightarrow {A'B'}\\ = \dfrac{1}{2}\left( {\overrightarrow {SA} + \overrightarrow {SB} } \right)\left( {\overrightarrow {SB'} - \overrightarrow {SA'} } \right)\\ = \dfrac{1}{2}\left( {\overrightarrow {SA} .\overrightarrow {SB'} - \overrightarrow {SA} .\overrightarrow {SA'} + \overrightarrow {SB} .\overrightarrow {SB'} - \overrightarrow {SB} .\overrightarrow {SA'} } \right).\end{array}\) Ta có \(\overrightarrow {SA} .\overrightarrow {SB'} = 0\) do \(SA \bot SB'\), \(\overrightarrow {SB} .\overrightarrow {SA'} = 0\) do \(SB \bot SA'\), \(\overrightarrow {SA} .\overrightarrow {SA'} = \overrightarrow {SB} .\overrightarrow {SB'} \). Từ đó suy ra \(\overrightarrow {SM} .\overrightarrow {A'B'} = 0\), nên \(SM \bot A'B'\). Sachbaitap.com
Xem thêm tại đây:
Bài 2. Tích vô hướng của hai vec tơ
|

 Tải ngay
Tải ngay