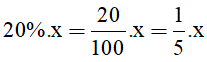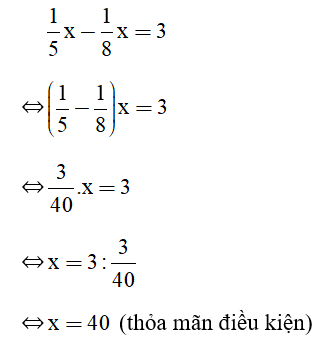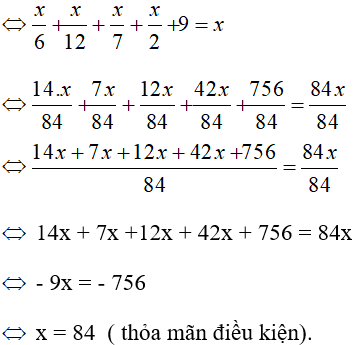Bài 34, 35, 36 trang 25, 26 SGK Toán 8 tập 2 - Giải bài toán bằng cách lập phương trìnhBài 34, 35 trang 25; bài 36 trang 26 SGK Toán 8 tập 2 - Giải bài toán bằng cách lập phương trình. Bài 36 (Bài toán nói về cuộc đời nhà toán học Đi-ô-phăng, lấy trong Hợp tuyển Hy Lạp - Cuốn sách gồm 46 bài toán về số, viết dưới dạng thơ trào phúng). Bài 34 trang 25 SGK Toán lớp 8 tập 2 Câu hỏi: Mẫu số của một phân số lớn hơn tử số của nó là 3 đơn vị. Nếu tăng cả tử và mẫu của nó thêm 2 đơn vị thì được phân số mới bằng \(\dfrac{1}{2}\) . Tìm phân số ban đầu. Phương pháp: B1: Đặt tử số là ẩn tìm điều kiện của ẩn và biểu diễn phân số đó theo ẩn. B2: Dựa vào dữ kiện của đề bài lập phương trình. B3: Giải phương trình. B4: Kết luận (Kiểm tra nghiệm tìm được có thỏa mãn các điều kiện của ẩn không)
Lời giải: Gọi x là tử số của phân số (x ∈ ℤ; x ≠ -3) Vì mẫu hơn tử số 3 đơn vị nên mẫu số là: x + 3. Phân số ban đầu là Nếu tăng cả tử và mẫu của nó thêm 2 đơn vị thì được phân số mới là: Theo giả thiết ta có: Suy ra: 2(x + 2) = 1.(x + 5) 2x + 4 = x + 5 x = 1 (thỏa mãn điều kiện) Do đó tử số của phân số là 1. Mẫu số của phân số là 1 + 3 = 4. Vậy phân số ban đầu là Bài 35 trang 25 SGK Toán lớp 8 tập 2 Câu hỏi: Học kì một, số học sinh giỏi của lớp 8A bằng 1/8 số học sinh cả lớp. Sang học kì hai, có thêm 3 bạn phấn đấu trở thành học sinh giỏi nữa, do đó số học sinh giỏi bằng 20% số học sinh cả lớp. Hỏi lớp 8A có bao nhiêu học sinh? Phương pháp: B1: Đặt số học sinh của cả lớp là ẩn, biểu diễn học sinh giỏi của mỗi kỳ theo ẩn đó. B2: Lập trình biểu diễn kết nối giữa các đại lượng B3: Set up the method. B4: Kết luận (Kiểm tra tìm kiếm được thỏa mãn các điều kiện của ẩn) Lời giải: Gọi số học sinh của lớp 8A là x (x ∈ N*; x > 3). Số học sinh giỏi của học kì I là : Sang học kì 2, số học sinh giỏi bằng 20% số học sinh cả lớp nên số học sinh giỏi của học kì II là : Vì số học sinh giỏi của học kì II nhiều hơn số HSG của học kì I 3 học sinh nên ta có :
Vậy lớp 8A có 40 học sinh. Bài 36 trang 26 SGK Toán lớp 8 tập 2 Câu hỏi: (Bài toán nói về cuộc đời nhà toán học Đi-ô-phăng, lấy trong Hợp tuyển Hy Lạp - Cuốn sách gồm 46 bài toán về số, viết dưới dạng thơ trào phúng).
Phương pháp: B1: Đặt số tuổi của ông Đi – ô – phăng là ẩn, đặt điều kiện cho ẩn B2: Biểu diễn các đại lượng còn lại theo ẩn. B3: Lập phương trình biểu diễn mối quan hệ giữa các đại lượng và giải phương trình đó. B4: Kết luận (Kiểm tra nghiệm tìm được có thỏa mãn các điều kiện của ẩn không) Lời giải: Gọi x là số tuổi của ông Đi-ô-phăng (x > 0, x ∈ N).
Vậy nhà toán học Đi-ô-phăng thọ 84 tuổi. sachbaitap.com
Xem thêm tại đây:
Chương III. Phương trình bậc nhất một ẩn
|
-

Bài 37, 38, 39 trang 30 SGK Toán 8 tập 2 - Giải bài toán bằng cách lập phương trình (tiếp)
Bài 37, 38, 39 trang 30 SGK Toán 8 tập 2 - Giải bài toán bằng cách lập phương trình (tiếp).Bài 37 trang 30 Lúc 6 giờ sáng, một xe máy khởi hành từ A để đến B. Sau đó 1 giờ, một ô tô cũng xuất phát từ A đến B với vận tốc trung bình lớn hơn vận tốc trung bình của xe máy 20km/h. Cả hai xe đến B đồng thời vào lúc 9 giờ 30 phút sáng cùng ngày. Tính độ dài quãng đường AB và vận tốc trung bình của xe máy
-

Bài 40, 41, 42, 43, 44, 45, 46, 47, 48, 49 trang 31, 32 SGK Toán 8 tập 2 - Luyện tập
Bài 40, 41, 42, 43, 44, 45, 46 trang 31; bài 47, 48, 49 trang 32 SGK Toán 8 tập 2 - Luyện tập. Bài 40 trang 31 Năm nay, tuổi mẹ gấp 3 lần tuổi Phương. Phương tính rằng 13 năm nữa thì tuổi mẹ chỉ còn gấp 2 lần tuổi Phương thôi. Hỏi năm nay Phương bao nhiêu tuổi?
-

Bài 50, 51, 52, 53, 54, 55, 56 trang 33, 34 SGK Toán 8 tập 2 - Ôn tập chương 3
Bài 50, 51, 52 trang 33; bài 53, 54, 55, 56 trang 34 SGK Toán 8 tập 2 - Ôn tập chương 3. Bài 54 trang 34: Một canô xuôi dòng từ bến A đến bến B mất 4 giờ và ngược dòng từ bến B về bến A mất 5 giờ. Tính khoảng cách giữa hai bến A và B, biết rằng vận tốc của dòng nước là 2 km/h.
-

Bài 1, 2, 3, 4 trang 37 SGK Toán 8 tập 2 - Liên hệ giữa thứ tự và phép cộng
Bài 1, 2, 3, 4 trang 37 SGK Toán 8 tập 2 - Liên hệ giữa thứ tự và phép cộng. Bài 4 trang 37 Đố: Một biển báo giao thông với nền trắng, số 20 màu đen, viền đỏ (xem minh họa ở hình bên) cho biết vận tốc tối đa mà các phương tiện giao thông được đi trên quãng đường có biển quy định là 20km/h. Nếu một ô tô đi trên đường đó có vận tốc là a (km/h) thì a phải thỏa mãn điều kiện nào trong các điều kiện sau?

 Tải ngay
Tải ngay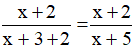 .
.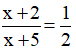 .
.