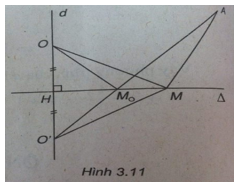
Bài 3.40 trang 161 Sách bài tập (SBT) Toán Hình học 10

Trong mặt phẳng Oxy cho đường thẳng \(\Delta :x - y + 2 = 0\) và điểm A(2;0).

a) Chứng mình rằng hai điểm A và O nằm về cùng một phía đối với đường thẳng .

b) Tìm điểm M trên \(\Delta \) sao cho độ dài đường gấp khúc OMA ngắn nhất.

Gợi ý làm bài

(h.3.11) 

Ta có:

\(\Delta \left( O \right) = 2 > 0\)

\(\Delta \left( A \right) = 2 + 2 > 0\)

Vậy A và O nằm về cùng một phía đối với \(\Delta \) 

b) Gọi O' là điểm đối xứng của O qua \(\Delta \), ta có:

\(OM + MA = O'M + MA \ge O'A\)

Ta có : OM + MA ngắn nhất

\( \Leftrightarrow O',M,A\) thẳng hàng 

Xét đường thẳng d đi qua O và vuông góc với  \(\Delta \) . Phương trình của d là: 

x + y = 0

d cắt \(\Delta \) tại H(-1;1).

H là trung điểm của OO' suy ra \(O'\left( { - 2;2} \right)\)

Phương trình đường thẳng O'A là: x + 2y - 2 = 0

Giải hệ phương trình 

\(\left\{ \matrix{
x + 2y = 2 \hfill \cr
x - y = - 2 \hfill \cr} \right.\)

ta được \(M = \left( { - {2 \over 3};{4 \over 3}} \right).\)

Sachbaitap.net