Bài 3.51 trang 132 sách bài tập (SBT) – Hình học 12Lập phương trình mặt phẳng (P) chứa đường thẳng d: và song song với d1: Lập phương trình mặt phẳng (P) chứa đường thẳng d: \(\left\{ {\matrix{{x = - 2 - t} \cr {y = 1 + 4t} \cr {z = 1 - t} \cr} } \right.\) và song song với d1: \({{x - 1} \over 1} = {{y - 1} \over 4} = {{z - 1} \over { - 3}}\) Hướng dẫn làm bài: Đường thẳng d đi qua M(-2; 1;1) có vecto chỉ phương là \(\overrightarrow a ( - 1;4; - 1)\) Đường thẳng d1 đi qua N(1; 1; 1) có vecto chỉ phương là \(\overrightarrow b (1;4; - 3)\) Ta có: \(\overrightarrow {MN} (3;0;0);\overrightarrow a \wedge \overrightarrow b = ( - 8; - 4; - 8)\) nên \(\overrightarrow {MN} (\overrightarrow a \wedge \overrightarrow b ) \ne 0\) , suy ra d và d1 chéo nhau. Do đó (P) là mặt phẳng đi qua M(-2; 1; 1) có vecto pháp tuyến bằng \(\overrightarrow a \wedge \overrightarrow b \) Phương trình của (P) là: \(–8(x + 2) – 4(y – 1) – 8(z – 1) = 0\) hay \(2x +y + 2z + 1 = 0\) Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
ÔN TẬP CHƯƠNG III - PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
|
-
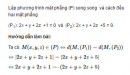
Bài 3.52 trang 132 sách bài tập (SBT) – Hình học 12
Lập phương trình mặt phẳng (P) song song và cách đều hai mặt phẳng (P1): 2x + y + 2z +1 = 0 và (P2): 2x + y + 2z +5 = 0.
-
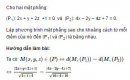
Bài 3.53 trang 132 sách bài tập (SBT) – Hình học 12
Cho hai mặt phẳng: (P1): 2x + y + 2z +1 = 0 và (P2): 4x – 2y – 4z + 7 = 0. Lập phương trình mặt phẳng sao cho khoảng cách từ mỗi điểm của nó đến (P1) và (P2) là bằng nhau.
-
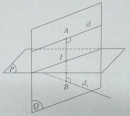
Bài 3.54 trang 132 sách bài tập (SBT) – Hình học 12
Cho hai đường thẳng d: và d1: Lập phương trình mặt phẳng (P) sao cho khoảng cách từ d và d1 đến (P) là bằng nhau.
-

Bài 3.55 trang 132 sách bài tập (SBT) – Hình học 12
Lập phương trình mặt phẳng (P) đi qua điểm M(1; -3; 2) và vuông góc với hai mặt phẳng (Q): 2x – y +3z + 1 = 0 và (R): x – 2y – z + 8 = 0

 Tải ngay
Tải ngay







