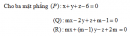Bài 40 trang 125 Sách bài tập Hình học lớp 12 Nâng cao

Bình chọn:

4.9 trên 7 phiếu

Viết phương trình mạt phẳng đi qua điểm

Viết phương trình mạt phẳng đi qua điểm M₀(1;1;1), cắt các tia Ox, Oy, Oz tại A, B, C, sao cho thể tích của tứ diện OABC có giá trị nhỏ nhất.

Giải

Giả sử \(A(a;0;0),B(0;b;0),C = (0;0;c)\) với \(a,b,c > 0\) và (P) là mặt phẳng phải tìm. Phương trình của (P) là :

\({x \over a} + {y \over b} + {z \over c} = 1.\)

Vì \({M_0} \in \left( P \right)\) nên \({1 \over a} + {1 \over b} + {1 \over c} = 1.\)

Thể tích của tứ diện OABC là : \({V_{OABC}} = {1 \over 6}abc.\)

Theo bất đẳng thức Cô-si :

\(1 = {1 \over a} + {1 \over b} + {1 \over c} \ge {3 \over {\root 3 \of {abc} }} \Leftrightarrow abc \ge 27\)

\( \Rightarrow {V_{OABC}} \ge {{27} \over 6} = {9 \over 2}\), dấu bằng xảy ra khi \(a=b=c=3.\)

Vậy V_OABC nhỏ nhất bằng \({9 \over 2}\) khi \(a=b=c=3\), khi đó phương trình mặt phẳng (P) là \(x+y+z-3=0.\)

Sachbaitap.com

Báo lỗi - Góp ý

Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.