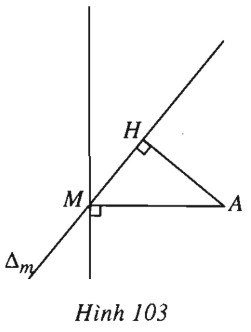
Bài 41 trang 106 SBT Hình học 10 Nâng cao

Cho đường thẳng \(\Delta _m\): \((m-2)x+(m-1)y+2m-1=0\) và hai điểm \(A(2 ; 3), B(1 ; 0).\)

a) Chứng minh rằng \(\Delta_m \) luôn đi qua một điểm cố định với mọi \(m;\)

b) Xác định \(m\) để \(\Delta_m \) có ít nhất một điểm chung với đoạn thẳng \(AB;\)

c) Tìm \(m\) để khoảng cách từ điểm \(A\) đến đường thẳng \(\Delta_m \) là lớn nhất.

Giải

a) \({\Delta _m}\) luôn đi qua điểm cố định \(M(x_0 ; y_0)\) với mọi \(m\) khi và chỉ khi

\(\begin{array}{l}(m - 2){x_0} + (m - 1){y_0} + 2m - 1 = 0  \,\,\,\,\,\forall m\\ \Leftrightarrow    ({x_0} + {y_0} + 2)m - 2{x_0} - {y_0} - 1 = 0  \,\,\,\,\, \forall m\\ \Leftrightarrow   \left\{ \begin{array}{l}{x_0} + {y_0} + 2 = 0\\ - 2{x_0} - {y_0} - 1 = 0\end{array} \right.     \Leftrightarrow    \left\{ \begin{array}{l}{x_0} = 1\\{y_0} =  - 3.\end{array} \right.\end{array}\)

Vậy \({\Delta _m}\) luôn đi qua điểm cố định \(M(1 ; -3)\) với mọi \(m\).

b) Đặt 

\(f(x,y) = (m - 2)x + (m - 1)y + 2m - 1 = 0\)

\({\Delta _m}\) có ít nhất một điểm chung với đoạn \(AB\) \( \Leftrightarrow   f({x_A} , {y_A}).f({x_B} , {y_B}) \le 0\)

\( \Leftrightarrow    (7m - 8)(3m - 3) \le 0 \)

\(     \Leftrightarrow     1 \le m \le  \dfrac{8}{7}\).

c) (h.103).

Dựng \(AH \bot {\Delta _m}\). Ta có \(AH \le AM\) với mọi \(m\) (\(M\) là điểm thuộc \({\Delta _m}\) với mọi \(m\) đã nói ở câu a). Vậy \(AH\) lớn nhất bằng \(AM\) khi và chỉ khi \(H\) trùng với \(M\) hay \(AM \bot {\Delta _m}\).

Ta có : \(\overrightarrow {AM}  = ( - 1 ;  - 6), {\Delta _m}\) có vec tơ chỉ phương \(\overrightarrow u (1 - m ; m - 2)\).

\(AM \bot {D_m}    \Leftrightarrow    \overrightarrow {AM} .\overrightarrow u  = 0 \)

\(    \Leftrightarrow     - 1(1 - m) - 6(m - 2) = 0 \)

\(    \Leftrightarrow    m =  \dfrac{{11}}{5}\).

Vậy với \(m =  \dfrac{{11}}{5}\) thì khoảng cách từ \(A\) đến \({\Delta _m}\) là lớn nhất.

Sachbaitap.com