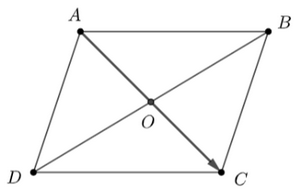
Bài 4.39, 4.40, 4.41, 4.42, 4.43, 4.44, 4.45, 4.46 trang 66, 67 SBT Toán 10 tập 1 Kết nối tri thức

A. TRẮC NGHIỆM

Bài 4.39 trang 66 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho hình bình hành \(ABCD\) tâm \(O.\) Xét các vectơ có hai điểm mút lấy từ các điểm \(A,\,\,B,\,\,C,\,\,D\) và \(O.\) Số các vectơ khác vectơ – không và cùng phương với \(\overrightarrow {AC} \) là:

A. 6

B. 3

C. 4

D. 2

Lời giải:

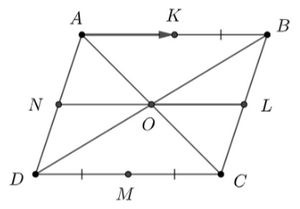
Các vectơ khác vectơ không và cùng phương với vectơ \(\overrightarrow {AC} \) là: \(\overrightarrow {AC} \), \(\overrightarrow {CA} \), \(\overrightarrow {AO} \), \(\overrightarrow {OA} \), \(\overrightarrow {OC} \), \(\overrightarrow {CO} \).

Có 6 vectơ cùng phương với vectơ \(\overrightarrow {AC} \).

Chọn A.

Bài 4.40 trang 66 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho đoạn thẳng \(AC\) và \(B\) là một điểm nằm giữa \(A,\,\,C.\) Trong các khẳng định sau, khẳng định nào là một khẳng định đúng?

A. Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CB} \) cùng hướng.

B. Hai vectơ \(\overrightarrow {CA} \) và \(\overrightarrow {BC} \) cùng hướng.

C. Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng hướng.

D. Hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BA} \) cùng hướng

Lời giải:

Chọn đáp án: C. Hai vectơ  và  cùng hướng.

Bài 4.41 trang 67 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho hình bình hành \(ABCD\) tâm \(O\). Gọi \(K,\,\,L,\,\,M,\,\,N\) tướng ứng là trung điểm các cạnh \(AB,\,\,BC,\,\,CD,\,\,DA.\) Trong các vectơ có đầu mút lấy từ các điểm \(A,\,\,B,\,\,C,\,\,D,\,\,K,\)\(L,\,\,M,\,\,O\) có bao nhiêu vectơ bằng vectơ \(\overrightarrow {AK} \) ?

A. 2

B. 6

C. 4

D. 8

Lời giải:

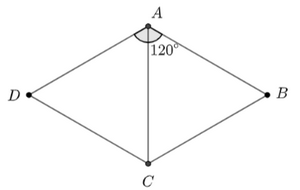
Xét hình bình hành \(ABCD\):

\( \Rightarrow \) \(AB = CD\)

mặt khác \(K\) và \(M\) lần lượt là trung điểm của \(AB\) và \(CD\)

nên \(AK = KB = CM = DM\)         (1)

Ta có: \(NL\) là đường trung bình của hình bình hành \(ABCD\)

\( \Rightarrow \) \(NL\)//\(AB\)

Mặt khác \(AN\)//\(BL\)

\( \Rightarrow \) tứ giác \(ABLN\) là hình bình hành

\( \Rightarrow \) \(AB = NL\)

Ta có: \(O\) là trung điểm của \(NL\)

\(K\) là trung điểm của \(AB\)

Mặt khác \(AB = NL\)

\( \Rightarrow \) \(AK = NO = OL = AB\)        (2)

Từ (1) và (2) \( \Rightarrow \) \(AK = KB = NO = OL = DM = MC\)

Mà các đường thẳng \(KB,\) \(NO,\) \(OL,\) \(DM,\) \(MC\) đều song song với \(AK\)

\( \Rightarrow \) \(\overrightarrow {AK}  = \overrightarrow {KB}  = \overrightarrow {NO}  = \overrightarrow {OL}  = \overrightarrow {DM}  = \overrightarrow {MC} \)

Có 6 vectơ bằng vectơ \(\overrightarrow {AK} \)

Chọn B.

Bài 4.42 trang 67 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho hình thoi \(ABCD\) có độ dài các cạnh bằng 1 và \(\widehat {DAB} = {120^ \circ }.\) Khẳng định nào sau đây là đúng?

A. \(\overrightarrow {AB}  = \overrightarrow {CD} \)

B. \(\overrightarrow {BD}  = \overrightarrow {AC} \)

C. \(\left| {\overrightarrow {BD} } \right| = 1\)

D. \(\left| {\overrightarrow {AC} } \right| = 1\)

Lời giải:

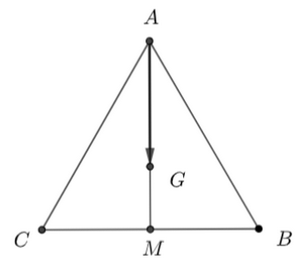
Xét hình thoi có: \(\widehat {DAB} = {120^ \circ }.\)

\( \Rightarrow \) \(\widehat {BAC} = \widehat {DAC} = {60^ \circ }\) (t/c)

Xét \(\Delta ABC\) có: \(BA = BC\)

\( \Rightarrow \) \(\Delta ABC\) cân tại \(B\)

Mặt khác \(\widehat {BAC} = {60^ \circ }\)

Nên \(\Delta ABC\) là tam giác đều

\( \Rightarrow \) \(AC = 1\) hay \(\left| {\overrightarrow {AC} } \right| = 1\)

Chọn D.

Bài 4.43 trang 67 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho tam giác \(ABC\) đều, trọng tâm \(G,\) có độ dài các cạnh bằng 3. Độ dài vectơ \(\overrightarrow {AG} \) bằng

A. \(\sqrt 3 \)

B. \(\frac{{3\sqrt 3 }}{2}\)

C. \(\frac{{\sqrt 3 }}{2}\)

D. \(2\sqrt 3 \)

Lời giải:

Gọi \(M\) là trung điểm của cạnh \(BC\)

\( \Rightarrow \) \(AM = \frac{{3\sqrt 3 }}{2}\)

Xét \(\Delta ABC\) đều có \(G\) là trọng tâm của tam giác

\( \Rightarrow \) \(\overrightarrow {AG}  = \frac{2}{3}\overrightarrow {AM} \)

\( \Rightarrow \left| {\overrightarrow {AG} } \right| = \frac{2}{3}\left| {\overrightarrow {AM} } \right| = \frac{2}{3}.\frac{{3\sqrt 3 }}{2} = \sqrt 3 \)

Chọn A.

Bài 4.44 trang 67 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho tam giác \(ABC\) vuông tại \(A\) và \(AB = 3,\,\,AC = 4.\) Độ dài của vectơ \(\overrightarrow {CB}  + \overrightarrow {AB} \) bằng

A. \(\sqrt {13} \)

B. \(2\sqrt {13} \)

C. \(4\)

D. \(2\)

Lời giải:

Ta có: \(\overrightarrow {CB}  + \overrightarrow {AB}  = \left( {\overrightarrow {AB}  - \overrightarrow {AC} } \right) + \overrightarrow {AB}  = 2\overrightarrow {AB}  - \overrightarrow {AC} \)

\( \Leftrightarrow \) \({\left| {\overrightarrow {CB}  + \overrightarrow {AB} } \right|^2} = {\left( {2\overrightarrow {AB}  - \overrightarrow {AC} } \right)^2} = 4{\overrightarrow {AB} ^2} - 4\overrightarrow {AB} .\overrightarrow {AC}  + {\overrightarrow {AC} ^2}\)

\( \Leftrightarrow \) \({\left| {\overrightarrow {CB}  + \overrightarrow {AB} } \right|^2} = 4{\overrightarrow {AB} ^2} + {\overrightarrow {AC} ^2} = 4.9 + 16 = 52\)

\( \Leftrightarrow \) \(\left| {\overrightarrow {CB}  + \overrightarrow {AB} } \right| = \sqrt {52}  = 2\sqrt {13} \)

Chọn B.

Bài 4.45 trang 67 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho tam giác \(ABC\) có \(AB = 2,\,\,BC = 4\) và \(\widehat {ABC} = {60^ \circ }.\) Độ dài của vectơ \(\overrightarrow {AC}  - \overrightarrow {BA} \) bằng

A. \(2\)

B. \(\sqrt {19} \)

C. \(4\)

D. \(\frac{{\sqrt {19} }}{2}\)

Lời giải:

Gọi \(M\) là trung điểm \(BC\)

\( \Rightarrow \) \(BM = \frac{1}{2}BC = 2\)

Xét \(\Delta ABM\) có: \(AB = BM = 2\)

\( \Rightarrow \) \(\Delta BAM\) cân tại \(B\)

Mà \(\widehat {ABM} = {60^ \circ }\)

\( \Rightarrow \) \(\Delta BAM\) đều

\( \Rightarrow \) \(AM = 2\)

Ta có: \(\left| {\overrightarrow {AC}  - \overrightarrow {BA} } \right| = \left| {\overrightarrow {AC}  + \overrightarrow {AB} } \right| = 2\left| {\overrightarrow {AM} } \right| = 2.2 = 4\)

Chọn C.

Bài 4.46 trang 67 SBT Toán lớp 10 tập 1 - Kết nối tri thức

Cho tam giác \(ABC\) và điểm \(I\) sao cho \(\overrightarrow {IB}  + 2\overrightarrow {IC}  = \overrightarrow 0 .\) Khẳng định nào sau đây là một khẳng định đúng?

A. \(\overrightarrow {AI}  = 2\overrightarrow {AC}  - \overrightarrow {AB} \)

B. \(\overrightarrow {AI}  = \overrightarrow {AB}  - 2\overrightarrow {AC} \)

C. \(\overrightarrow {AI}  = \frac{{\overrightarrow {AB}  - 2\overrightarrow {AC} }}{{ - 3}}\)

D. \(\overrightarrow {AI}  = \frac{{\overrightarrow {AB}  + 2\overrightarrow {AC} }}{3}\)

Lời giải:

Ta có: \(\overrightarrow {IB}  + 2\overrightarrow {IC}  = \overrightarrow 0 \)

\( \Leftrightarrow \) \(\left( {\overrightarrow {AB}  - \overrightarrow {AI} } \right) + 2\left( {\overrightarrow {AC}  - \overrightarrow {AI} } \right) = \overrightarrow 0 \)

\( \Leftrightarrow \) \(\overrightarrow {AB}  + 2\overrightarrow {AC}  - 3\overrightarrow {AI}  = \overrightarrow 0 \)

\( \Leftrightarrow \) \(\overrightarrow {AI}  = \frac{{\overrightarrow {AB}  + 2\overrightarrow {AC} }}{3}\)

Chọn D.

Sachbaitap.com