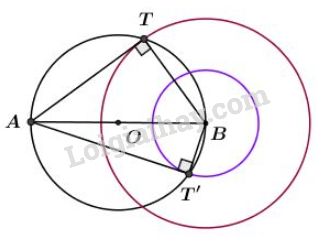
Bài 48, 49, 50, 51, 52 trang 87 SGK Toán 9 tập 2 - Luyện tậpGiải bài 48, 49, 50, 51, 52 trang 87 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Luyện tập Cung chứa góc. bài 50 Cho đường tròn đường kính AB cố định, M là một điểm chạy trên đường tròn. Trên tia đối của tia MA lấy điểm I sao cho MI = 2MB. Bài 48 trang 87 SGK Toán lớp 9 tập 2 Câu hỏi: Cho hai điểm \(A, B\) cố định. Từ \(A\) vẽ các tiếp tuyến với đường tròn tâm \(B\) bán kính không lớn hơn \(AB\). Tìm quỹ tích các tiếp điểm. Lời giải:
Dự đoán: Quỹ tích là đường tròn đường kính AB. + Phần thuận: Tiếp tuyến \(TA\) vuông góc với bán kính \(BT\) tại tiếp điểm \(T\). Suy ra \( \widehat{ATB}=90^0\) Do \(AB\) cố định nên quỹ tích của \(T\) là đường tròn đường kính \(AB\). + Phần đảo: Lấy T thuộc đường tròn đường kính AB \( \Rightarrow \widehat {ATB} = {90^0}\) ( Góc nội tiếp chắn nửa đường tròn) ⇒ AT ⊥ TB và BT < AB ⇒ AT tiếp xúc với đường tròn tâm B, bán kính BT < BA. Kết luận: Quỹ tích các tiếp điểm là đường tròn đường kính AB. Bài 49 trang 87 SGK Toán lớp 9 tập 2 Câu hỏi: Dựng tam giác \(ABC,\) biết \(BC = 6cm,\) \(\widehat{A}=40^0\) và đường cao \(AH = 4cm.\) Lời giải:
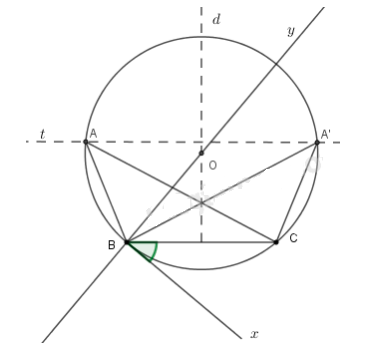
Cách dựng: + Kẻ đoạn thẳng \(AB = 6cm\) + Dựng cung chứa góc \(40^\circ \) trên đoạn \(BC.\) - Vẽ đường trung trực d của đoạn \(BC\) - Vẽ tia \(Bx\) tạo với \(BC\) góc \(40^\circ \) - Vẽ tia \(By \bot Bx\), tia \(By\) cắt đường thẳng \(d\) tại \(O.\) Vẽ cung \(BmC\) tâm \(O\) bán kính \(OB\) sao cho cung này nằm ở nửa mặt phẳng bờ \(BC\) không chứa \(Bx\). Cung \(BmC\) chính là cung chứa góc \(40^\circ \) cần dựng. + Vẽ đường thẳng \(t\) song song với \(BC\) và cách \(BC\) một khoảng \(4cm.\) Gọi giao điểm của đường thẳng \(t\) với cung \(BmC\) là \(A\) và \(A'.\) Khi đó có hai tam giác thỏa mãn đề bài là \(ABC\) hoặc tam giác \(A'BC.\) Chứng minh: + Theo cách dựng có BC = 6cm. + A ∈ cung chứa góc 40º dựng trên đoạn BC \(\Rightarrow \widehat {BAC} = {40^0}\) + A ∈ t song song với BC và cách BC 4cm nên chiều cao của tam giác ABC là 4cm. Vậy ΔABC thỏa mãn yêu cầu đề bài. Biện luận: Vì t cắt cung \(BmC\) tại 2 điểm nên bài toán có 2 nghiệm hình Bài 50 trang 87 SGK Toán lớp 9 tập 2 Câu hỏi: Cho đường tròn đường kính \(AB\) cố định. \(M\) là một điểm chạy trên đường tròn. Trên tia đối của tia \(MA\) lấy điểm \(I\) sao cho \(MI = 2MB.\) a) Chứng minh \(\widehat{AIB}\) không đổi. b) Tìm tập hợp các điểm \(I\) nói trên. Phương pháp: a) Sử dụng góc nội tiếp chắn nửa đường tròn là góc vuông và tỉ số lượng giác của góc nhọn b) Chứng minh theo hai phần: Phần thuận và phần đảo. Lập luận để có quỹ tích là cung chứa góc \(AIB\) dựng trên đoạn BC. Chú ý đến giới hạn của quỹ tích. Lời giải: 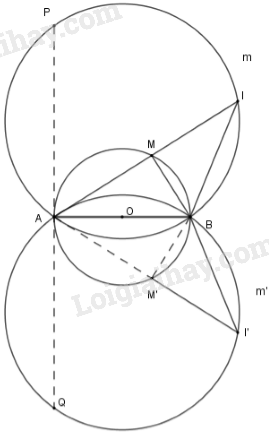
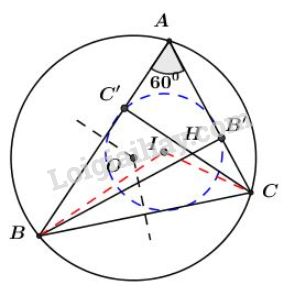
a) Gọi \(O\) là trung điểm \(AB\). Xét đường tròn tâm \(O\) có \(\widehat {AMB}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {AMB} = 90^\circ \) hay \(AM \bot MB\) Xét tam giác vuông \(MBI\) có \(MI = 2MB \Rightarrow \tan \widehat {MIB} = \dfrac{{MB}}{{MI}} = \dfrac{{MB}}{{2MB}} = \dfrac{1}{2}\) \(\Rightarrow \widehat {AIB} = \alpha =26^{0}34'\) không đổi b) Phần thuận: Khi điểm M thay đổi trên đường tròn đường kính AB thì điểm I thay đổi và luôn nhìn cạnh AB dưới một góc \(\widehat {AIB} = \alpha =26^{0}34'\) không đổi Vậy điểm I thuộc hai cung chứa góc \(\alpha=26^{0}34' \) dựng trên đoạn AB. Nhưng tiếp tuyến PQ với đường tròn đường kính AB tại A là vị trí giới hạn của AM. Do đó điểm I thuộc hai cung \(PmB,Qm'B\). Hai điểm P, Q là các điểm giới hạn của quỹ tích, điểm B là điểm đặc biệt của quỹ tích Phần đảo: Lấy điểm \(I'\) bất kỳ thuộc cung \(Qm'B\) (hoặc cung \(PmB\)). Nối \(AI'\) cắt đường tròn tâm \(O\) tại \(M'.\) Ta chứng minh \(M'I' = 2M'B.\) Xét \(\left( O \right)\) có \(\widehat {AM'B}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {AM'B} = 90^\circ \Rightarrow AM' \bot BM' \Rightarrow \widehat {BM'I'} = 90^\circ \) Xét tam giác \(BM'I'\) vuông ở \(M'\) có \(\widehat {BI'M'} = \alpha \) (do \(I'\) bất kỳ thuộc cung \(Qm'B\) là cung chứa góc \(\alpha \) dựng trên đoạn AB) nên \(\tan \widehat {BI'M'} = \tan \alpha = \dfrac{1}{2}\) mà \(\tan \widehat {BI'M'} = \dfrac{{BM'}}{{M'I'}} \Rightarrow \dfrac{{BM'}}{{M'I'}} = \dfrac{1}{2} \Rightarrow M'I' = 2BM'\) Kết luận: Quỹ tích các điểm I là hai cung \(PmB,Qm'B\). Bài 51 trang 87 SGK Toán lớp 9 tập 2 Câu hỏi: Cho \(I, \, O\) lần lượt là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp tam giác \(ABC\) với \(\widehat{A} = 60^0.\) Gọi \(H\) là giao điểm của các đường cao \(BB'\) và \(CC'.\) Chứng minh các điểm \(B,\, C,\, O,\, H,\, I\) cùng thuộc một đường tròn. Lời giải:
+) Ta có: \(\widehat{BOC} = 2\widehat{BAC} = 2.60^0= 120^0\) (góc nội tiếp và góc ở tâm cùng chắn một cung \(BC\)). (1) +) Lại có \(\widehat{BHC} = \widehat{B'HC'}\) (hai góc đối đỉnh) Xét tứ giác AB'HC' có: \(\widehat{B'HC'} + \widehat {HC'A} + \widehat {HB'A} + \widehat A = 360^0\) (tổng các góc của tứ giác bằng \(360^0\)) nên \(\widehat{B'HC'} = 360^\circ - \widehat {HC'A} - \widehat {HB'A} - \widehat A\) \( = 360^\circ - 90^\circ - 90^\circ - 60^\circ = 120^\circ\) \(\Rightarrow \widehat{BHC} = 120^0.\) (2) +) Vì I là tâm đường tròn nội tiếp tam giác ABC nên BI; CI lần lượt là tia phân giác góc B, góc C. Xét tam giác \(ABC\) có \(\widehat B + \widehat C + \widehat A = 180^\circ \) (Định lí tổng 3 góc trong một tam giác) \( \Leftrightarrow \widehat B + \widehat C = 180^\circ - 60^\circ = 120^\circ \) Xét tam giác BIC có \(\widehat {BIC}+ \widehat {IBC}+ \widehat {ICB}=180^0\) (Định lí tổng 3 góc trong một tam giác) \(\Rightarrow \)\(\begin{array}{l}\widehat {BIC} = 180^\circ - \widehat {IBC} - \widehat {ICB} = 180^\circ - \dfrac{{\widehat B}}{2} - \dfrac{{\widehat C}}{2}\\ = 180^\circ - \dfrac{{\widehat B + \widehat C}}{2} = 180^\circ - 60^\circ = 120^\circ \end{array}\) Do đó \(\widehat{BIC} = 120^0.\) (3) Từ (1), (2), (3) ta thấy các điểm \(O, \, H, \, I\) cùng nằm trên các cung chứa góc \(120^0\) dựng trên đoạn thẳng \(BC.\) hay 5 điểm \(B,\, C,\, O,\, H,\, I\) cùng thuộc một đường tròn. Bài 52 trang 87 SGK Toán lớp 9 tập 2 Câu hỏi: "Góc sút" của quả phạt đền \(11\) mét là bao nhiêu độ? Biết rằng chiều rộng cầu môn là \(7,32m.\) Hãy chỉ ra hai vị trí khác trên sân có cùng "góc sút" như quả phạt đền \(11 m.\) Lời giải:
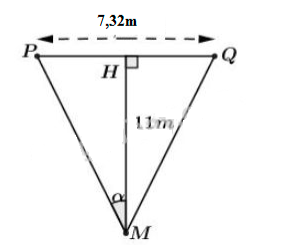
Gọi vị trí đặt bóng để sút phạt đền là \(M,\) và bề ngang cầu môn là \(PQ\) thì \(M\) nằm trên đường trung trực của \(PQ\). Gọi \(H\) là trung điểm \(PQ,\) thì \(PH = \dfrac{PQ}{2} = \dfrac{7,32}{2} = 3,66\) \(\widehat{PMH} = \alpha.\) Do M nằm trên đường trung trực của PQ nên MH \(\bot\) PQ. Áp dụng tỉ số lượng giác trong tam giác vuông MPH, ta có: \(tan α = \dfrac{3,66}{11}≈ 0,333 \Rightarrow α = 18^036’\). Vậy góc sút phạt đền là \(2α=2. 18^036' ≈ 37^012’\). Vẽ cung chứa góc \(37^0 12’\) dựng trên đoạn thẳng \(PQ.\) Bất cứ điểm nào trên cung vừa vẽ cũng có “góc sút” như quả phạt đền \(11m.\) Sachbaitap.com
Xem thêm tại đây:
Bài 6. Cung chứa góc
|
-

Bài 53, 54, 55 trang 89 SGK Toán 9 tập 2 - Tứ giác nội tiếp
Giải bài 53, 54, 55 trang 89 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Tứ giác nội tiếp. Bài 54 Tứ giác ABCD có góc ABC + góc ADC = 180o. Chứng minh rằng các đường trung trực của AC, BD, AB cùng đi qua một điểm
-

Bài 56, 57, 58, 59, 60 trang 89, 90 SGK Toán 9 tập 2 - Luyện tập
Giải bài 56, 57 trang 89; bài 58, 59, 60 trang 90 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Luyện tập - Tứ giác nội tiếp. Bài 59 Cho hình bình hành ABCD. Đường tròn đi qua ba đỉnh A, B, C cắt đường thẳng CD tại P khác C. Chứng minh AP = AD.

 Tải ngay
Tải ngay