Bài 51 trang 108 SBT Hình học 10 Nâng cao

Viết phương trình đường thẳng $\Delta$ tiếp xúc với đường tròn $(C)$ tại $A  \in  (C)$ trong mỗi trường hợp sau rồi sau đó vẽ $\Delta$ và $(C)$ trên cùng hệ trục tọa độ

a) $(C): {x^2} + {y^2} = 25 ;$ $A(3 ; 4) ;$

b) $(C): {x^2} + {y^2} = 100 ;$ $A( - 8 ; 6);$

c) $(C): {x^2} + {y^2} = 50 ;$ $A(5 ;  - 5);$

d) ${x^2} + {y^2} = 80 ;$ $A( - 4 ;  - 8) ;$

e) ${(x - 3)^2} + {(y + 4)^2} = 169 ;$  $A(8 ;  - 16)$;

f) $(C): {(x + 5)^2} + {(y - 9)^2} = 289 ;$ $A( - 13 ;  - 6).$

Giải

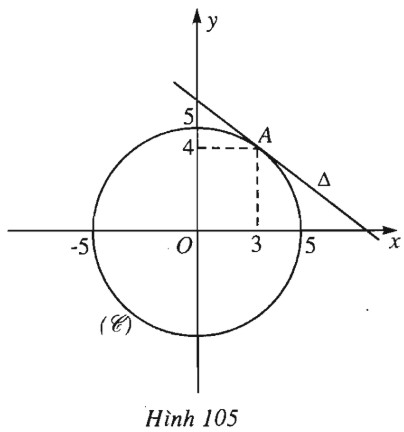
a) $(C)$ có tâm $O(0 ; 0)$, bán kính $R = 5$. Tiếp tuyến $\Delta$ đi qua A, nhận $\overrightarrow {OA} (3 ; 4)$ làm vec tơ pháp tuyến nên có phương trình

$3(x - 3) + 4(y - 4) = 0$

$\Leftrightarrow    3x + 4y - 25 = 0$.

Đường tròn $(C)$ và tiếp tuyến $\Delta$ được vẽ như hình 105. Các câu còn lại làm tương tự.

Sachbaitap.com