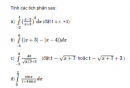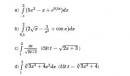Bài 5.18 trang 222 sách bài tập (SBT) - Giải tích 12Giải các bất phương trình sau: Giải các bất phương trình sau: a) \({(0,5)^{{1 \over x}}} \ge 0,0625\) b) \({\log _{0,2}}({x^2} - 4) \ge - 1\) c) \({\log _2}{\log _{0,5}}({2^x} - {{15} \over {16}}) \le 2\) d) \({\log _3}({16^x} - {2.12^x}) \le 2x + 1\) Hướng dẫn làm bài: a) Bất phương trình đã cho tương đương với \({({1 \over 2})^{{1 \over x}}} \ge {1 \over {16}} \Leftrightarrow {({1 \over 2})^{{1 \over x}}} \ge {({1 \over 2})^4}\) \(\Leftrightarrow {1 \over x} \le 4 \Leftrightarrow {1 \over x} - 4 \le 0 \Leftrightarrow {{1 - 4x} \over x} \le 0 \Leftrightarrow \left[ {\matrix{{x \ge {1 \over 4}} \cr {x < 0} \cr} } \right.\) b) Điều kiện: \(\left[ {\matrix{{x > 2} \cr {x < - 2} \cr} } \right.\) Bất phương trình đã cho tương đương với \({\log _{0,2}}({x^2} - 4) \ge {\log _{0,2}}0,{2^{ - 1}} = {\log _{0,2}}5\) \( \Leftrightarrow {x^2} - 4 \le 5\) (vì 0,2 < 1) \( \Leftrightarrow {x^2} - 9 \le 0 \Leftrightarrow - 3 \le x \le 3\) Kết hợp với điều kiện, ta được \(\left[ {\matrix{{2 < x \le 3} \cr { - 3 \le x < - 2} \cr} } \right.\) c) Bất phương trình đã cho tương đương với \(0 < {\log _{0,5}}({2^x} - {{15} \over {16}}) \le 4\) \( \Leftrightarrow 1 > {2^x} - {{15} \over {16}} \ge 0,{5^4}\) \(\Leftrightarrow {{31} \over {16}} > {2^x} \ge 1\) \(\Leftrightarrow {\log _2}{{31} \over {16}} > x \ge 0\) \( \Leftrightarrow 0 \le x < {\log _2}31 - 4\) Ở đây, chúng ta đã áp dụng tính đồng biến và nghịch biến của các hàm số logarit và hàm số mũ với cơ số lớn hơn 1 và nhỏ hơn 1. d) Bất phương trình đã cho tương đương với \(0 < {16^x} - {2.12^x} \le {3^{2x + 1}}\) \(\Leftrightarrow 0 < {4^x}{.4^x} - {2.4^x}{.3^x} \le {3^x}{.3^x}.3\) \(\Leftrightarrow 0 < {({4 \over 3})^{2x}} - 2{({4 \over 3})^x} \le 3\) (1) (Ta đã chia cả hai vế cho \({9^x}\;\left( {{9^x} > {\rm{ }}0{\rm{ }}} \right)\)) Đặt \({({4 \over 3})^x} = t(t > 0)\) , ta có hệ bất phương trình: \(\left\{ {\matrix{{{t^2} - 2t \le 3} \cr {{t^2} - 2t > 0} \cr {t > 0} \cr} } \right.\) \(\Leftrightarrow \left\{ {\matrix{{t > 0} \cr {{t^2} - 2t - 3 \le 0} \cr {{t^2} - 2t > 0} \cr} } \right.\) \(\Leftrightarrow \left\{ {\matrix{{t > 0} \cr { - 1 \le t \le 3} \cr {\left[ {\matrix{{t > 2} \cr {t < 0} \cr} } \right.} \cr} } \right. \Leftrightarrow 2 < t \le 3\) Từ đó, ta có \(2 < {({4 \over 3})^x} \le 3 < = > {\log _{{4 \over 3}}}2 < x \le {\log _{{4 \over 3}}}3\). Sachbaitap.com6
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
BÀI TẬP ÔN TẬP CUỐI NĂM - GIẢI TÍCH 12
|
-
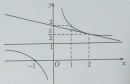
Bài 5.21 trang 223 sách bài tập (SBT) - Giải tích 12
Tính diện tích của hình phẳng giới hạn bởi các đường sau:
-
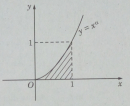
Bài 5.22 trang 223 sách bài tập (SBT) - Giải tích 12
Tính thể tích của vật thể tròn xoay khi quay các hình phẳng giới hạn bởi các đường sau quanh trục Ox:

 Tải ngay
Tải ngay