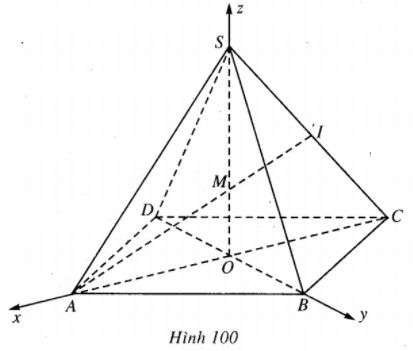
Bài 53 trang 127 Sách bài tập Hình học lớp 12 Nâng caoCho hình chóp tứ giác đều S.ABCD Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng h. Gọi I là trung điểm của cạnh bên SC. Tính khoảng cách từ điểm S đến mặt phẳng (ABI). Giải
Ta chọn hệ trục Oxyz sao cho gốc tọa độ là tâm O của đáy, tia Ox chứa OA, tia Oy chứa OB, tia Oz chứa OS. Khi đó : \(\eqalign{ & A = \left( {{{a\sqrt 2 } \over 2};0;0} \right), \cr & B = \left( {0;{{a\sqrt 2 } \over 2};0} \right) \cr & C = \left( { - {{a\sqrt 2 } \over 2};0;0} \right), \cr & S = (0;0;h) \cr} \) Rõ ràng giao điểm M của SO và AI chính là trọng tâm tam giác SAC nên \(M\left( {0;0;{h \over 3}} \right)\) Mặt phẳng (ABI) cũng chính là mặt phẳng (ABM). Vậy \(mp\left( {ABI} \right)\) có phương trình là : \({x \over {{{a\sqrt 2 } \over 2}}} + {y \over {{{a\sqrt 2 } \over 2}}} + {z \over {{h \over 3}}} = 1.\) Do đó, khoảng cách từ S tới mặt phẳng (ABI) là : \(d = {{\left| {{h \over {{h \over 3}}} - 1} \right|} \over {\sqrt {{{\left( {{1 \over {{{a\sqrt 2 } \over 2}}}} \right)}^2} + {{\left( {{1 \over {{{a\sqrt 2 } \over 2}}}} \right)}^2} + {{\left( {{1 \over {{h \over 3}}}} \right)}^2}} }} = {2 \over {\sqrt {{2 \over {{a^2}}} + {2 \over {{a^2}}} + {9 \over {{h^2}}}} }} \) \(\Rightarrow d = {{2ah} \over {\sqrt {4{h^2} + 9{a^2}} }}.\) Sachbaitap.com
Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 2. Phương trình mặt phẳng
|
-
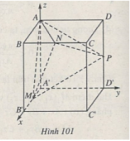
Bài 54 trang 127 Sách bài tập Hình học lớp 12 Nâng cao
Cho khối lập phương ABCD.A’B’C’D’ cạnh bằng 1.
-
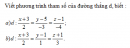
Bài 55 trang 130 Sách bài tập Hình học lớp 12 Nâng cao
Viết phương trình tham số của đường thẳng d, biết :
-
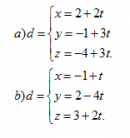
Bài 56 trang 130 Sách bài tập Hình học lớp 12 Nâng cao
Viết phương trình chính tắc của đường thẳng d biết :
-

Bài 57 trang 130 Sách bài tập Hình học lớp 12 Nâng cao
Viết phương trình tham số hoặc chính tắc của đường thẳng d biết :

 Tải ngay
Tải ngay