Bài 57 trang 130 Sách bài tập Hình học lớp 12 Nâng caoViết phương trình tham số hoặc chính tắc của đường thẳng d biết : Viết phương trình tham số hoặc chính tắc của đường thẳng d biết : a) d là giao tuyến của hai mặt phẳng \(\left( \alpha \right):x - 3y + z = 0\) và \(\left( {\alpha '} \right):x + y - z + 4 = 0\) b) d là giao tuyến của mặt phẳng \(y-2z+3=0\) với mặt phẳng tọa độ (Oyz). Giải a) Cách 1. Điểm M(x; y; z)\( \in d\) khi tọa độ của M là nghiệm của hệ \(\left\{ \matrix{ x - 3y + z = 0 \hfill \cr x + y - z + 4 = 0 \hfill \cr} \right.\) Đặt y=t ta có \(\left\{ \matrix{ x + z = 3t \hfill \cr x - z = - 4 - t \hfill \cr} \right. \Rightarrow \left\{ \matrix{ x = - 2 + t \hfill \cr z = 2 + 2t. \hfill \cr} \right.\) Vậy phương trình tham số của d là : \(\left\{ \matrix{ x = - 2 + t \hfill \cr y = t \hfill \cr z = 2 + 2t. \hfill \cr} \right.\) Cách 2. Ta tìm một điểm thuộc đường thẳng d bằng cách cho y=0 trong hệ \(\left( * \right).\) Ta có hệ \(\left\{ \matrix{ x + z = 0 \hfill \cr x - z = - 4 \hfill \cr} \right. \Rightarrow \left\{ \matrix{ x = - 2 \hfill \cr z = 2. \hfill \cr} \right.\) Vậy điểm \({M_0}( - 2;0;2)\) thuộc đường thẳng d. Vectơ chỉ phương của đường thẳng d là \(\overrightarrow u = \left( {\left| \matrix{ - 3 \hfill \cr 1 \hfill \cr} \right.\left. \matrix{ 1 \hfill \cr - 1 \hfill \cr} \right|;\left| \matrix{ 1 \hfill \cr - 1 \hfill \cr} \right.\left. \matrix{ 1 \hfill \cr 1 \hfill \cr} \right|;\left| \matrix{ 1 \hfill \cr 1 \hfill \cr} \right.\left. \matrix{ - 3 \hfill \cr 1 \hfill \cr} \right|} \right) = (2;2;4)\) Vậy phương trình tham số của d là \(d:\left\{ \matrix{ x = - 2 + 2t \hfill \cr y = 2t \hfill \cr z = 2 + 4t. \hfill \cr} \right.\) b) Mặt phẳng (Oyz): \(x=0\) tương tự câu a ta tìm được giao tuyến d có phương trình là: \(\;d:\left\{ \matrix{ x = 0 \hfill \cr y = - 3 + 2t \hfill \cr z = t. \hfill \cr} \right.\) Sachbaitap.com
Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 3. Phương trình đường thẳng - SBT Toán 12 Nâng cao
|
-

Bài 59 trang 130 Sách bài tập Hình học lớp 12 Nâng cao
Viết phương trình đường thẳng trong mỗi trường hợp sau đây :
-
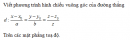
Bài 60 trang 131 Sách bài tập Hình học lớp 12 Nâng cao
Viết phương trình hình chiếu vuông góc của đường thẳng
-

Bài 61 trang 131 Sách bài tập Hình học lớp 12 Nâng cao
a)Viết phương trình hình chiếu của đường thẳng d :

 Tải ngay
Tải ngay








