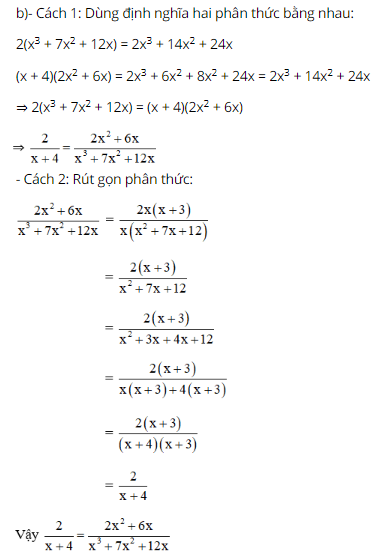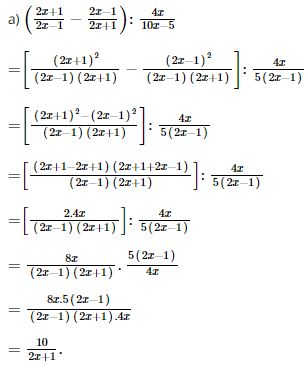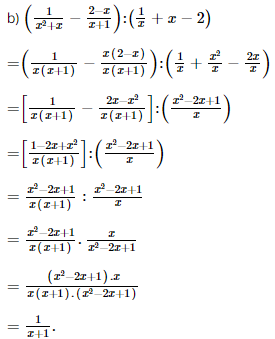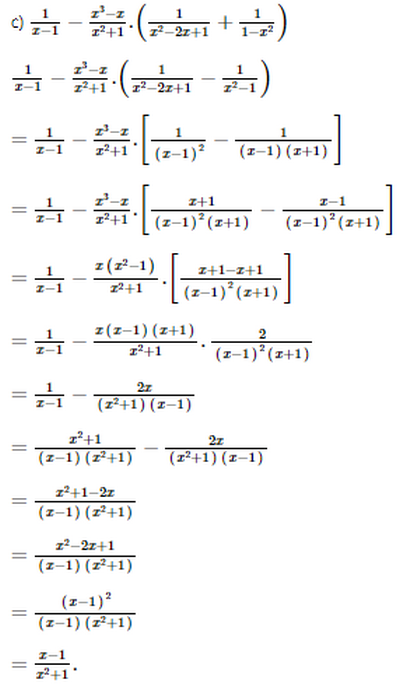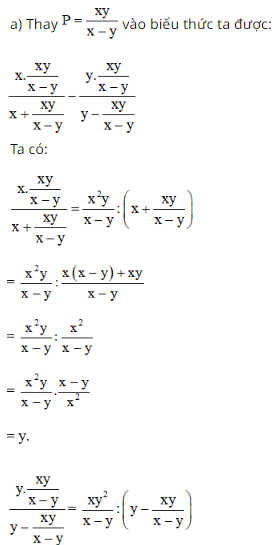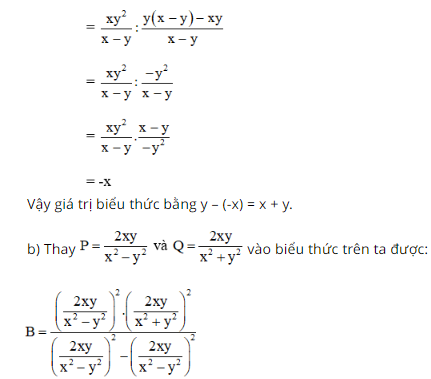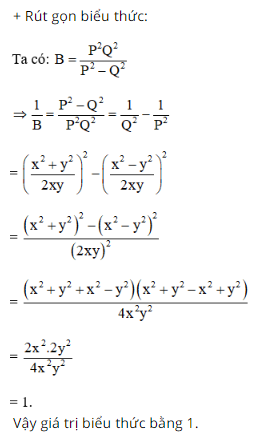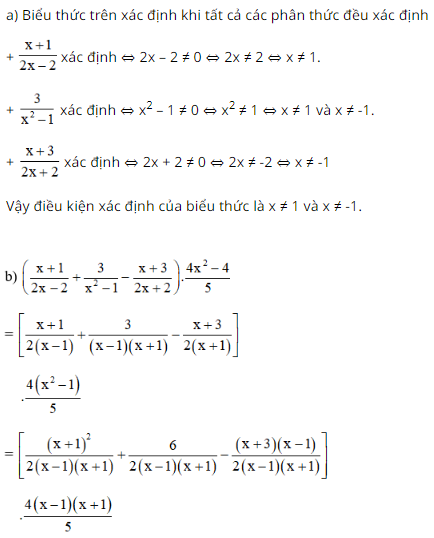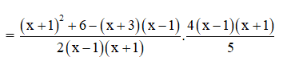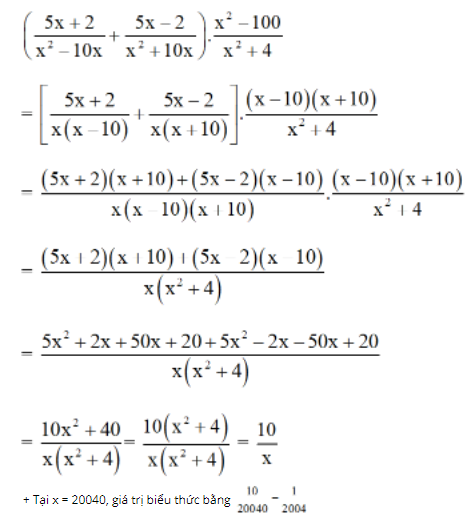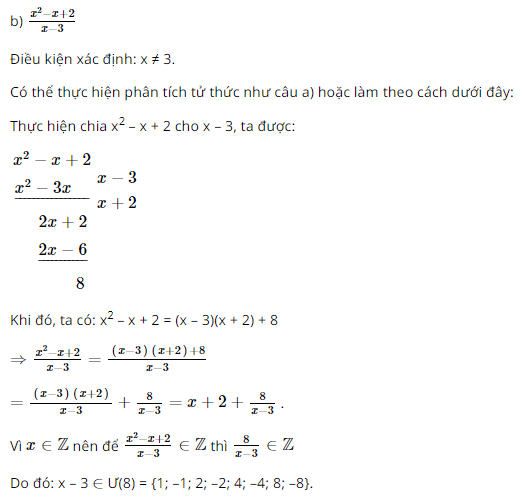Bài 57, 58, 59, 60, 61, 62, 63, 64 trang 61, 62 SGK Toán 8 tập 1 - Ôn tập chương 2

Bài 57 trang 61 SGK Toán lớp 8 tập 1

Câu hỏi:

Chứng tỏ mỗi cặp phân thức sau bằng nhau:

a.\ (\ dfrac {3} {{2x - 3}} \) và \ (\ dfrac {{3x + 6}} {{2 {x ^ 2} + x - 6}} \);

b.\(\dfrac{2}{{x + 4}}\) và \(\dfrac{{2{x^2} + 6x}}{{{x^3} + 7{x^2} + 12x}}\).

Phương pháp:

Cách 1: Dùng định nghĩa hai phân thức bằng nhau:

Hai phân thức \( \dfrac {A}{B}\) và \( \dfrac {C}{D} \)  gọi là bằng nhau nếu \(AD=BC \).

Cách 2: Rút gọn phân thức đại số.

Lời giải:

Bài 58 trang 62 SGK Toán lớp 8 tập 1

Câu hỏi:

 Thực hiện các phép tính sau:

a.\ (\ eqalign {
& \, \, \ left ({{{2x + 1} \ over {2x - 1}} - {{2x - 1} \ over {2x + 1}}} \ right): {{ 4x} \ trên {10x - 5}} \ cr} \)

b. \ (\ eqalign {
& \, \, \ left ({{1 \ over {{x ^ 2} + x}} - {{2 - x} \ over {x + 1}}} \ right): \ left ({{1 \ over x} + x - 2} \ right) \ cr} \)

c.\ (\ eqalign { 
& {\ rm {}} {1 \ over {x - 1}} - {{{x ^ 3} - x} \ over {{x ^ 2} + 1}}. \ left ({ {1 \ over {{x ^ 2} - 2x + 1}} + {1 \ over {1 - {x ^ 2}}}} \ right). \ Cr} \)

Phương pháp:

Áp dụng:

- Đại số phân thức, trừ, nhân, chia quy tắc.

- Chú ý đến việc thực hiện các phép tính tự động: Thực hiện trong ngoặc trước, nhân chia trước cộng trừ sau.

Lời giải:

Bài 59 trang 62 SGK Toán lớp 8 tập 1

Câu hỏi:

 a. Cho biểu thức  \(\dfrac{{xP}}{{x + P}} - \dfrac{{yP}}{{y - P}}\). Thay \(P = \dfrac{{xy}}{{x - y}}\) vào biểu thức đã cho rồi rút gọn biểu thức.

b.Cho biểu thức \(\dfrac{{{P^2}{Q^2}}}{{{P^2} - {Q^2}}}\). Thay \(P = \dfrac{{2xy}}{{{x^2} - {y^2}}}\) và \(Q = \dfrac{{2xy}}{{{x^2} + {y^2}}}\) vào biểu thức đã cho rồi rút gọn biểu thức.

Phương pháp:

a. Thay đa thức \(P\) vào biểu thức đã cho rồi áp dụng các quy tắc cộng, trừ, nhân, chia đa thức để rút gọn biểu thức.

b. Thay các đa thức \(P, \; Q\) vào biểu thức đã cho rồi áp dụng các quy tắc cộng, trừ, nhân, chia đa thức để rút gọn biểu thức. 

Lời giải:

Bài 60 trang 62 SGK Toán lớp 8 tập 1

Câu hỏi:

Lời giải:

Bài 61 trang 62 SGK Toán lớp 8 tập 1

Câu hỏi:

Tìm điều kiện của \(x\) để giá trị của biểu thức \(\left( {\dfrac{{5x + 2}}{{{x^2} - 10x}} + \dfrac{{5x - 2}}{{{x^2} + 10x}}} \right).\dfrac{{{x^2} - 100}}{{{x^2} + 4}}\) được xác định.

Tính giá trị của biểu thức tại \(x = 20 040\).

Phương pháp:

- Phân thức đại số của biến \(x\) có dạng \( \dfrac{A(x)}{B(x)}\)  được xác định khi \(B(x) \ne 0\).

- Để tính giá trị của biểu thức được đơn giản hơn ta rút gọn biểu thức trước sau đó thay giá trị của \(x\) và biểu thức đã được thu gọn.

Lời giải:

Bài 62 trang 62 SGK Toán lớp 8 tập 1

Câu hỏi:

  Tìm giá trị của \(x\) để giá trị của phân thức \(\dfrac{{{x^2} - 10x + 25}}{{{x^2} - 5x}}\) bằng \(0\).

Phương pháp:

- Phân thức đại số của biến \(x\) có dạng \( \dfrac{A(x)}{B(x)}\)  được xác định khi \(B(x) \ne 0\).

- Áp dụng tính chất:  phân thức \( \dfrac{A(x)}{B(x)}=0\) khi \(A(x) = 0\), (điều kiện \(B(x) \ne 0\)).

Lời giải:

Bài 63 trang 62 SGK Toán lớp 8 tập 1

Câu hỏi:

 Viết mỗi phân thức sau dưới dạng tổng của một đa thức và một phân thức với tử thức là một hằng số, rồi tìm các giá trị nguyên của \(x\) để giá trị của phân thức cũng là số nguyên:

a.\(\dfrac{{3{x^2} - 4x - 17}}{{x + 2}}\);

b. \(\dfrac{{{x^2} - x + 2}}{{x - 3}}\)

Phương pháp:

 Để giá trị của phân thức là số nguyên thì tử thức chia hết cho mẫu thức.

Lời giải:

Bài 64 trang 62 SGK Toán lớp 8 tập 1

Câu hỏi:

 Tìm giá trị của phân thức trong bài tập \(62\) tại \(x = 1,12\) và làm tròn kết quả đến chữ số thập phân thứ ba. 

Phương pháp:

 Thay \(x = 1,12\) vào phân thức sau khi rút gọn rồi tính giá trị của phân thức đó.

Lời giải:

Sachbaitap.com