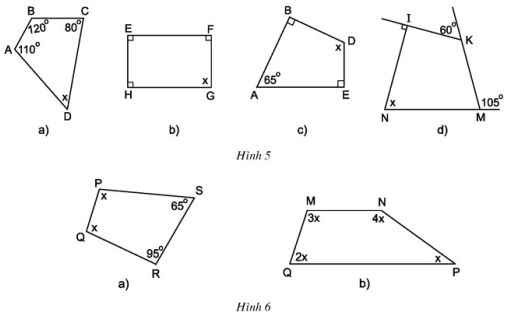
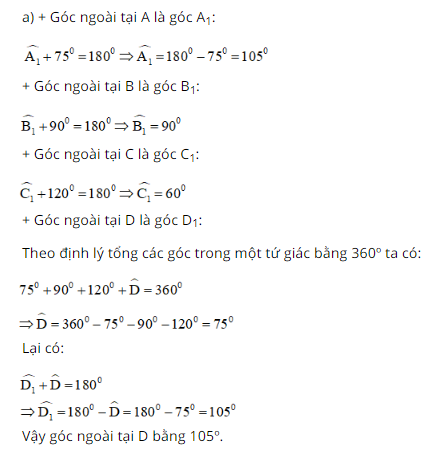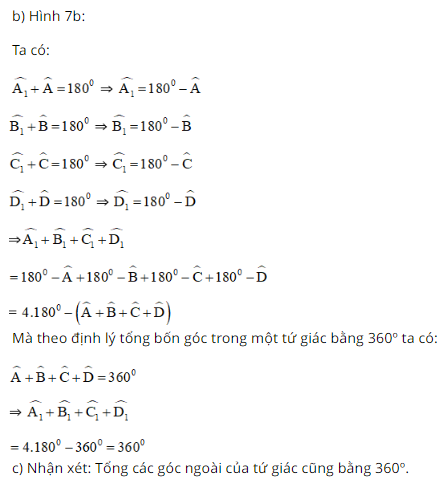Bài 1, 2, 3, 4, 5 trang 66, 67 SGK Toán 8 tập 1 - Tứ giácBài 1, 2 trang, bài 3, 4, 5 trang 67 SGK Toán 8 tập 1 - Tứ giác. Bài 4 Dựa vào cách vẽ các tam giác đã học, hãy vẽ lại các tứ giác ở hình (9), hình (10) vào vở. Bài 1 trang 66 SGK Toán lớp 8 tập 1 Câu hỏi: Tìm x ở hình 5, hình 6:
Phương pháp: Áp dụng định lý: Tổng các góc của một tứ giác bằng \(360^0.\) Lời giải: Ta có định lý: Tổng bốn góc trong một tứ giác bằng 360º.
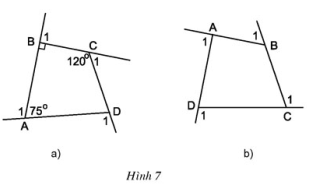
Bài 2 trang 66 SGK Toán lớp 8 tập 1 Câu hỏi: Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác. a. Tính các góc ngoài của tứ giác ở hình 7a. b.Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài): \(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = ?\) c. Có nhận xét gì về tổng các góc ngoài của tứ giác?
Phương pháp: a và b.Áp dụng định lý: Tổng các góc trong tứ giác bằng \({360^0}\) c. Áp dụng tính chất: Tổng hai góc kề bù bằng \({180^0}\) Lời giải:
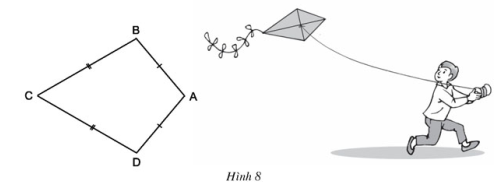
Bài 3 trang 67 SGK Toán lớp 8 tập 1 Câu hỏi: Ta gọi tứ giác \(ABCD\) trên hình \(8\) có \(AB = AD, CB = CD\) là hình "cái diều" a. Chứng minh rằng \(AC\) là đường trung trực của \(BD.\) b. Tính \(\widehat B;\widehat D\) biết rằng \(\widehat A = {100^0};\widehat C = {60^0}\).
Phương pháp: a. Áp dụng: Tính chất: Một điểm thuộc đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó. b. Áp dụng: - Định lý: Tổng các góc của một tứ giác bằng \({360^0}\) - Tính chất hai tam giác bằng nhau. Lời giải:
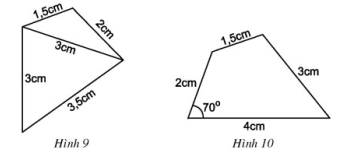
Bài 4 trang 67 SGK Toán lớp 8 tập 1 Câu hỏi: Dựa vào cách vẽ các tam giác đã học, hãy vẽ lại các tứ giác ở hình \(9\), hình \(10\) vào vở.
Phương pháp: - Áp dụng cách vẽ tam giác biết độ dài \(3\) cạnh, \(2\) cạnh và \(1\) góc xen giữa. Lời giải:
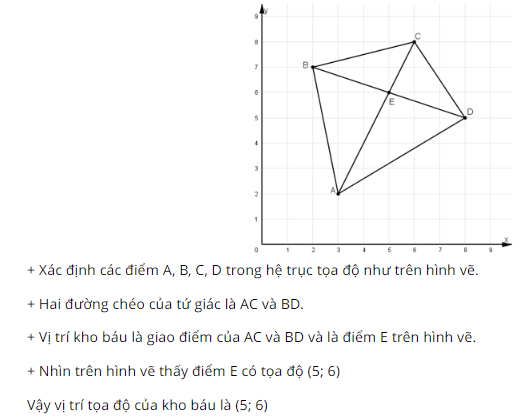
Bài 5 trang 67 SGK Toán lớp 8 tập 1 Câu hỏi: giác \(ABCD\), trong đó các đỉnh của tứ giác có tọa độ như sau: \(A(3 ; 2), B(2 ; 7), C(6 ; 8), D(8 ; 5).\)
Phương pháp: - Áp dụng cách xác định tọa độ của một điểm trên hệ trục tọa độ \(Oxy.\) Lời giải:
Sachbaitap.com
Xem thêm tại đây:
Chương I. Tứ giác
|
-

Bài 6, 7, 8, 9,10 trang 70, 71 SGK Toán 8 tập 1 - Hình thang
Bài 6 trang 70,bài 7, 8, 9,10 trang 71 SGK Toán 8 tập 1 - Hình thang. Bài 9 Tứ giác (ABCD) có (AB= BC) và (AC) tia phân giác của góc (A). Chứng minh rằng (ABCD) là hình thang.
-
Bài 11, 12, 13, 14, 15 trang 74, 75 SGK Toán 8 tập 1 - Hình thang cân
Bài 11, 12, 13 trang 74, bài 14, 15 trang 75 SGK Toán 8 tập 1 - Hình thang cân. Bài 12. Cho hình thang cân ABCD; (AB // CD, AB < CD) Kẻ đường cao (AE, BF) của hình thang. Chứng minh rằng (DE = CF.)
-

Bài 16, 17, 18, 19 trang 75 SGK Toán 8 tập 1 - Luyện tập
Bài 16, 17, 18, 19 trang 75 SGK Toán 8 tập 1 - Luyện tập. Bài Cho tam giác (ABC) cân tại (A), các đường phân giác (BD, CE) ((D ∈ AC, E ∈ AB)). Chứng minh rằng (BEDC) là hình thang cân có đáy nhỏ bằng cạnh bên.
-

Bài 20, 21, 22, 23, 24, 25 trang 79, 80 SGK Toán 8 tập 1 - Đường trung bình của tam giác, của hình thang
Bài 20, 21 trang 79, bài 22, 23, 24, 25 trang 80 SGK Toán 8 tập 1 - Đường trung bình của tam giác, của hình thang. Bài 24 Hai điểm (A) và (B) thuộc cùng một nửa mặt phẳng có bờ là đường (xy.) Khoảng cách từ điểm (A) đến (xy) bằng (12,cm), khoảng cách từ điểm (B) đến (xy) bằng (20,cm.) Tính khoảng cách từ trung điểm (C) của (AB) đến (xy.)

 Tải ngay
Tải ngay