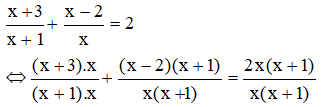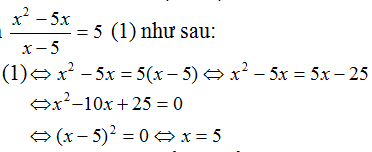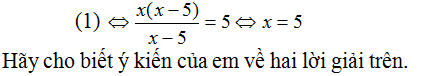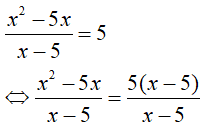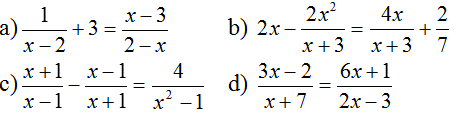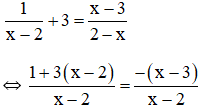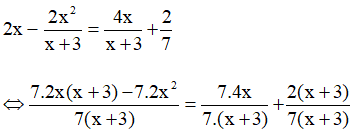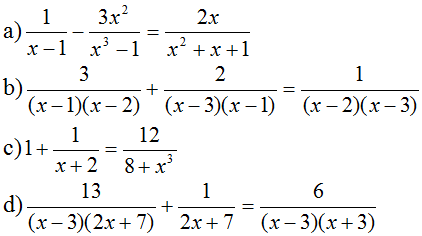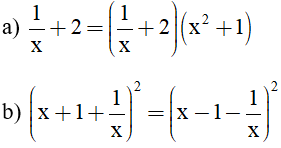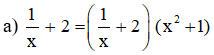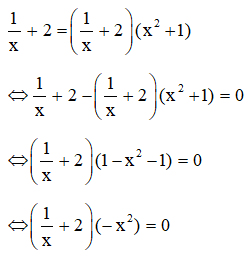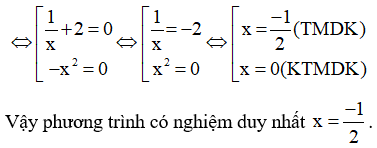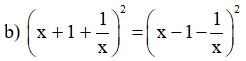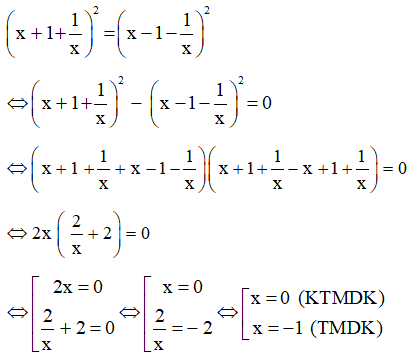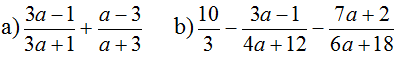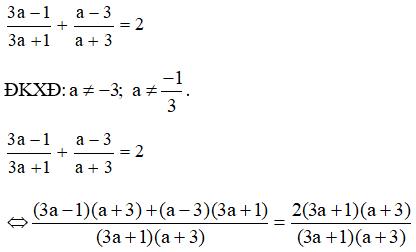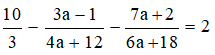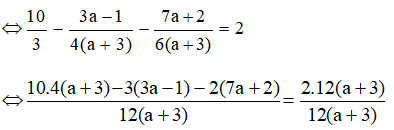Bài 27, 28, 29, 30, 31, 32, 33 trang 22, 23 SGK Toán 8 tập 2 - Phương trình chứa ẩn ở mẫuBài 27, 28, 29 trang 22; 30, 31, 32, 33 trang 23 SGK Toán 8 tập 2 - Phương trình chứa ẩn ở mẫu. Bài 33 Tìm các giá trị của a sao cho mỗi biểu thức sau có giá trị bằng 2: Bài 27 trang 22 SGK Toán lớp 8 tập 2 Câu hỏi: Giải các phương trình:
Phương Pháp: Giải phương trình chứa ẩn ở mẫu Bước 1: Tìm điều kiện xác định của phương trình Bước 2: Quy đồng mẫu hai vế của phương trình rồi khử mẫu. Bước 3: Giải phương trình vừa nhận được. Bước 4: Kết luận. Lời giải: a) Điều kiện xác định: x ≠ -5.
Suy ra: 2x – 5 = 3(x + 5) ⇔ 2x – 5 = 3x + 15 ⇔ -5 – 15 = 3x – 2x ⇔ x = -20 (thỏa mãn điều kiện xác định). Vậy phương trình có tập nghiệm S = {-20}. b) Điều kiện xác định: x ≠ 0.
Suy ra: 2(x2 – 6) = 2x2 + 3x ⇔ 2x2 – 12 – 2x2 – 3x = 0 ⇔ - 12 - 3x = 0 ⇔ -3x = 12 ⇔ x = -4 (thỏa mãn điều kiện xác định) Vậy phương trình có tập nghiệm S = {-4}. c) Điều kiện xác định: x ≠ 3.
Suy ra: (x2 + 2x) – (3x + 6) = 0 ⇔ x(x + 2) – 3(x + 2) = 0 ⇔ (x – 3)(x + 2) = 0 ⇔ x – 3 = 0 hoặc x + 2 = 0 + x – 3 = 0 ⇔ x = 3 (Không thỏa mãn đkxđ) + x + 2 = 0 ⇔ x = -2 (Thỏa mãn đkxđ). Vậy phương trình có tập nghiệm S = {-2}. d) Điều kiện xác định: x ≠ -2/3.
Suy ra: 5 = (2x – 1)(3x + 2) hay (2x – 1)(3x + 2) = 5 ⇔ 2x.3x + 2x.2 – 1.3x – 1.2 = 5 ⇔ 6x2 + 4x – 3x – 2 – 5 = 0 ⇔ 6x2 + x – 7 = 0. ⇔ 6x2 – 6x + 7x – 7 = 0 (Tách để phân tích vế trái thành nhân tử) ⇔ 6x(x – 1) + 7(x – 1) = 0 ⇔ (6x + 7)(x – 1) = 0 ⇔ 6x + 7 = 0 hoặc x – 1 = 0 + 6x + 7 = 0 ⇔ 6x = - 7 ⇔ x = -7/6 (thỏa mãn đkxđ) + x – 1 = 0 ⇔ x = 1 (thỏa mãn đkxđ). Vậy phương trình có tập nghiệm Bài 28 trang 22 SGK Toán lớp 8 tập 2 Câu hỏi: Giải các phương trình:
Lời giải: a) Điều kiện xác định: x ≠ 1.
Suy ra: 2x – 1 + x – 1 = 1 ⇔ 3x – 2 = 1 ⇔ 3x = 3 ⇔ x = 1 (không thỏa mãn điều kiện xác định). Vậy phương trình vô nghiệm. b) Điều kiện xác định: x ≠ -1.
Suy ra: 5x + 2( x+ 1) = - 12 ⇔ 5x + 2x + 2 = -12 ⇔ 7x + 2 = -12 ⇔ 7x = -14 ⇔ x = -2 (thỏa mãn đkxđ) Vậy phương trình có tập nghiệm S = {-2} c) Điều kiện xác định: x ≠ 0.
Suy ra: x3 + x = x4 + 1 ⇔ x4 + 1 – x – x3 = 0 ⇔ (x4 – x3) + (1 – x) = 0 ⇔ x3(x – 1) – (x – 1) = 0 ⇔ (x3 – 1)(x – 1) = 0 ⇔ (x – 1)(x2 + x + 1)(x – 1) = 0 ⇔ (x – 1)2. (x2 + x + 1) = 0 ⇔ x – 1 = 0 (vì ⇔ x = 1 (thỏa mãn đkxđ). Vậy phương trình có tập nghiệm S = {1}. d) Điều kiện xác định: x ≠ 0 và x ≠ -1.
Suy ra: x(x + 3) + (x + 1)(x – 2) = 2.x(x + 1) ⇔ x(x + 3) + (x + 1)(x – 2) – 2x(x + 1) = 0 ⇔ x2 + 3x + x2 – 2x + x – 2 – (2x2 + 2x) = 0 ⇔ x2 + 3x + x2 – 2x + x – 2 – 2x2 - 2x = 0 ⇔ x2 + x2 – 2x2 + 3x + x – 2x – 2x – 2 = 0 ⇔ 0x – 2 = 0 ⇔ 0x = 2 (vô lí) Phương trình vô nghiệm. Kiến thức áp dụng Để giải phương trình chứa ẩn ở mẫu ta cần: + Bước 1: Tìm điều kiện xác định (các mẫu thức khác 0). + Bước 2: Quy đồng mẫu số cả hai vế của phương trình rồi khử mẫu. + Bước 3: Giải phương trình vừa nhận được (Đưa về pt bậc nhất, đưa về pt tích; …) + Bước 4: Đối chiếu nghiệm với đkxđ rồi kết luận. Bài 29 trang 22 SGK Toán lớp 8 tập 2 Câu hỏi: Bạn Sơn giải phương trình
Bạn Hà cho rằng Sơn giải sai vì đã nhân hai vế với biểu thức x – 5 có chứa ẩn. Hà giải bằng cách rút gọn vế trái như sau:
Phương pháp: Phương pháp chứa ẩn ở mẫu Bước 1: Tìm xác định điều kiện của trình phương pháp Bước 2: Quy đồng mẫu của phương trình rồi khử mẫu. Bước 3: Đã nhận được Medium method. Bước 4: Kết luận. Lời giải: +) Cách làm của bạn Sơn sai vì chưa đặt điều kiện xác định cho phương trình đã nhân cả hai vế với ( x- 5). +) Cách làm của bạn Hà sai vì chưa đặt điều kiện xác định cho phương trình đã rút gọn cả hai vế cho biểu thức (x- 5) phụ thuộc biến x. +) Cách giải đúng Điều kiện xác định: x ≠ 5 Ta có:
Suy ra: x2 – 5x = 5( x- 5) x( x- 5) – 5(x – 5) = 0 ( x- 5).( x- 5) =0 (x - 5)2 = 0 x – 5= 0 x = 5 ( không thỏa mãn ĐKXĐ). Vậy phương trình đã cho vô nghiệm. Bài 30 trang 23 SGK Toán lớp 8 tập 2 Câu hỏi: Giải các phương trình:
Lời giải: a) Điều kiện xác định: x ≠ 2.
Suy ra: 1 + 3(x – 2) = -(x – 3) ⇔ 1 + 3x – 6 = -x + 3 ⇔ 3x + x = 3 + 6 – 1 ⇔ 4x = 8 ⇔ x = 2 (không thỏa mãn đkxđ). Vậy phương trình vô nghiệm. b) Điều kiện xác định: x ≠ -3.
Suy ra: 14x(x + 3) – 14x2 = 28x + 2(x + 3) ⇔ 14x2 + 42x – 14x2 = 28x + 2x + 6 ⇔ 42x – 28x – 2x = 6 ⇔ 12x = 6 ⇔ x = 12">1212. (thỏa mãn điều kiện) Vậy phương trình có tập nghiệm S = {12">1212}. c) Điều kiện xác định: x ≠ ±1. 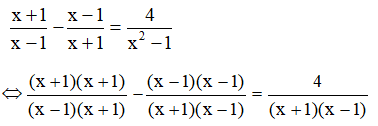 Suy ra: x2 + 2x + 1 – (x2 – 2x + 1) = 4 ⇔ x2 + 2x + 1 – x2 + 2x – 1 = 4 ⇔ 4x = 4 ⇔ x = 1 (không thỏa mãn đkxđ) Vậy phương trình vô nghiệm. d) Điều kiện xác định: x ≠ -7; x ≠ 32">3232. 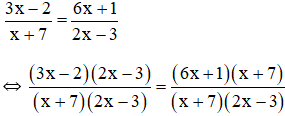 Suy ra: (3x – 2)(2x – 3) = (6x + 1)(x + 7) ⇔ 6x2 – 9x – 4x + 6 = 6x2 + 42x + x + 7 ⇔ - 4x - 9x - 42x - x = 7 - 6 ⇔ - 56x = 1 ⇔ x = −156">−156−156 (thỏa mãn đkxđ) Vậy phương trình có tập nghiệm S = {−156">−156−156}. Kiến thức áp dụng Để giải phương trình chứa ẩn ở mẫu ta cần: + Bước 1: Tìm điều kiện xác định (các mẫu thức khác 0). + Bước 2: Quy đồng mẫu số cả hai vế của phương trình rồi khử mẫu. + Bước 3: Giải phương trình vừa nhận được (Đưa về pt bậc nhất, đưa về pt tích; …) + Bước 4: Đối chiếu nghiệm với đkxđ rồi kết luận. Bài 31 trang 23 SGK Toán lớp 8 tập 2 Câu hỏi: Giải các phương trình:
Lời giải: a.\(\dfrac{1}{{x - 1}} - \dfrac{{3{x^2}}}{{{x^3} - 1}} = \dfrac{{2x}}{{{x^2} + x + 1}}\) (1) Ta có: \(x - 1 ≠ 0 \Leftrightarrow x ≠ 1\) và \({x^3} - 1 \ne 0\) khi \(x^3 \ne 1\) hay \(x \ne 1\) \( {x^2+x + 1} = {{x^2} + x + \dfrac{1}{4} + \dfrac{3}{4}} \) \( = {{x^2} + 2.x.\dfrac{1}{2} + {{\left( {\dfrac{1}{2}} \right)}^2} + \dfrac{3}{4}}\) \(= {{{\left( {x + \dfrac{1}{2}} \right)}^2} + \dfrac{3}{4}}\) Ta có: \({\left( {x + \dfrac{1}{2}} \right)^2} \geqslant 0\) với mọi \(x \in\mathbb R\) nên \({\left( {x + \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} > 0\) với mọi \(x \in\mathbb R\) Do đó: ĐKXĐ: \(x ≠ 1\) MTC= \({x^3} - 1=(x-1)(x^2+x+1)\) Ta có: (1) \( \Leftrightarrow \dfrac{{{x^2} + x + 1}}{{{x^3} - 1}} - \dfrac{{3{x^2}}}{{{x^3} - 1}} = \dfrac{{2x\left( {x - 1} \right)}}{{{x^3} - 1}}\) \(\Rightarrow {x^2} + x + 1 - 3{x^2} = 2x\left( {x - 1} \right) \) \(\Leftrightarrow - 2{x^2} + x + 1 = 2{x^2} - 2x\) \( \Leftrightarrow 0 = 2{x^2} - 2x + 2{x^2} - x - 1\) \( \Leftrightarrow 0 = 4{x^2} - 3x - 1\) \(\Leftrightarrow 4{x^2} - 3x - 1 = 0\) \(\Leftrightarrow 4{x^2} - 4x+x - 1 = 0\) \(\Leftrightarrow 4x\left( {x - 1} \right) + \left( {x - 1} \right) = 0\) \(\Leftrightarrow \left( {x - 1} \right)\left( {4x + 1} \right) = 0\) \( \Leftrightarrow \left[ \begin{gathered} \( \Leftrightarrow \left[ \begin{gathered} \(\Leftrightarrow \left[ {\matrix{{x = 1}\text{( loại)} \cr {x = - \dfrac{1}{4}}\text{(thỏa mãn)}\cr} }\right.\) Vậy phương trình có nghiệm duy nhất \(x = - \dfrac{1}{4}\) b.\(\dfrac{3}{{\left( {x - 1} \right)\left( {x - 2} \right)}} + \dfrac{2}{{\left( {x - 3} \right)\left( {x - 1} \right)}} \)\(\,= \dfrac{1}{{\left( {x - 2} \right)\left( {x - 3} \right)}}\) (2) ĐKXĐ: \(x ≠ 1, x ≠ 2, x ≠ 3\) MTC= \((x-1)(x-2)(x-3)\) Ta có: (2)
\( \Rightarrow 3\left( {x - 3} \right) + 2\left( {x - 2} \right) = x - 1\) \(\Leftrightarrow 3x - 9 + 2x - 4 = x - 1\) \( \Leftrightarrow 5x - 13 = x - 1\) \( \Leftrightarrow 5x - x = - 1 + 13\) \(⇔ 4x = 12\) \( \Leftrightarrow x = 12:4\) \(⇔ x = 3\) (không thỏa mãn ĐKXĐ) Vậy phương trình vô nghiệm. c. \(1 + \dfrac{1}{{x + 2}} = \dfrac{{12}}{{8 + {x^3}}}\)(3) Ta có: \(8 + {x^3} \ne 0\)\(\Leftrightarrow x^3 ≠ -8 ⇔ x ≠ -2\) ĐKXĐ: \(x ≠ -2\) MTC= \(8 + {x^3}=(x+2)(x^2-2x+4)\) Ta có: (3) \( \Leftrightarrow \dfrac{{8 + {x^3}}}{{8 + {x^3}}} + \dfrac{{{x^2} - 2x + 4}}{{8 + {x^3}}} = \dfrac{{12}}{{8 + {x^3}}}\) \( \Rightarrow {x^3} + 8 + {x^2} - 2x + 4 = 12 \) \( \Leftrightarrow {x^3} + {x^2} - 2x = 12 - 8 - 4\) \(\Leftrightarrow {x^3} + {x^2} - 2x = 0\) \(\Leftrightarrow x\left( {{x^2} + x - 2} \right) = 0\) \(\Leftrightarrow x\left[ {{x^2} + 2x - x - 2} \right] = 0\) ⇔\(x[ x(x+2) - (x+2) ] = 0\) ⇔ \(x(x + 2)(x - 1) = 0\) \( \Leftrightarrow \left[ \begin{array}{l} \(\Leftrightarrow \left[ \begin{array}{l} Vậy phương trình có tập nghiệm là \(S = \left\{ {0;1} \right\}\). d. \(\dfrac{{13}}{{\left( {x - 3} \right)\left( {2x + 7} \right)}} + \dfrac{1}{{2x + 7}} \)\(\,= \dfrac{6}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\) (4) ĐKXĐ: \(x \ne 3,x \ne - 3,x \ne - \dfrac{7}{2}\) MTC= \({\left( {x - 3} \right)\left( {x + 3} \right)}\left( {2x + 7} \right)\) Ta có: (4)
\( \Rightarrow 13\left( {x + 3} \right) + \left( {x - 3} \right)\left( {x + 3} \right) \)\(= 6\left( {2x + 7} \right) \) \(\Leftrightarrow 13x + 39 + {x^2} - 9 = 12x + 42\) \(\Leftrightarrow {x^2} + 13x + 30 = 12x + 42\) \( \Leftrightarrow {x^2} + 13x + 30 - 12x - 42 = 0\) \(\Leftrightarrow {x^2} + x - 12 = 0\) \(\Leftrightarrow {x^2} + 4x - 3x - 12 = 0\) \(\Leftrightarrow x\left( {x + 4} \right) - 3\left( {x + 4} \right) = 0\) \(\Leftrightarrow \left( {x - 3} \right)\left( {x + 4} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l} \(\Leftrightarrow \left[ \begin{array}{l} Vậy phương trình có tập nghiệm là \(S = \left\{-4 \right\}\). Bài 32 trang 23 SGK Toán lớp 8 tập 2 Câu hỏi: Giải các phương trình:
Lời giải:
ĐKXĐ: x ≠ 0
ĐKXĐ: x ≠ 0
Vậy nghiệm của phương trình là x = −1. Bài 33 trang 23 SGK Toán lớp 8 tập 2 Câu hỏi: Tìm các giá trị của a sao cho mỗi biểu thức sau có giá trị bằng 2:
Lời giải:
Suy ra: (3a – 1)(a + 3) + (a – 3)(3a + 1) = 2(3a + 1)(a + 3) ⇔ 3a2 + 9a – a – 3 + 3a2 + a – 9a – 3 = 2(3a2 + 9a + a + 3) ⇔ 6a2– 6 = 6a2 + 18a + 2a + 6 ⇔ 6a2– 6 − 6a2 − 18a − 2a – 6 = 0 ⇔ −20a – 12 = 0 ⇔ −20a = 12 ⇔ a = (thỏa mãn điều kiện) Vậy với a = thì biểu thức đã cho có giá trị bằng 2. b) Để biểu thức có giá trị bằng 2 thì ĐKXĐ: a ≠ -3 ta có:
Suy ra: (3a – 1)(a + 3) + (a – 3)(3a + 1) = 2(3a + 1)(a + 3) ⇔ 3a2 + 9a – a – 3 + 3a2 + a – 9a – 3 = 2(3a2 + 9a + a + 3) ⇔ 6a2– 6 = 6a2 + 18a + 2a + 6 ⇔ 6a2– 6 − 6a2 − 18a − 2a – 6 = 0 ⇔ −20a – 12 = 0 ⇔ −20a = 12 ⇔ a = Vậy với a = Sachbaitap.com
Xem thêm tại đây:
Chương III. Phương trình bậc nhất một ẩn
|
-

Bài 34, 35, 36 trang 25, 26 SGK Toán 8 tập 2 - Giải bài toán bằng cách lập phương trình
Bài 34, 35 trang 25; bài 36 trang 26 SGK Toán 8 tập 2 - Giải bài toán bằng cách lập phương trình. Bài 36 (Bài toán nói về cuộc đời nhà toán học Đi-ô-phăng, lấy trong Hợp tuyển Hy Lạp - Cuốn sách gồm 46 bài toán về số, viết dưới dạng thơ trào phúng).
-

Bài 37, 38, 39 trang 30 SGK Toán 8 tập 2 - Giải bài toán bằng cách lập phương trình (tiếp)
Bài 37, 38, 39 trang 30 SGK Toán 8 tập 2 - Giải bài toán bằng cách lập phương trình (tiếp).Bài 37 trang 30 Lúc 6 giờ sáng, một xe máy khởi hành từ A để đến B. Sau đó 1 giờ, một ô tô cũng xuất phát từ A đến B với vận tốc trung bình lớn hơn vận tốc trung bình của xe máy 20km/h. Cả hai xe đến B đồng thời vào lúc 9 giờ 30 phút sáng cùng ngày. Tính độ dài quãng đường AB và vận tốc trung bình của xe máy
-

Bài 40, 41, 42, 43, 44, 45, 46, 47, 48, 49 trang 31, 32 SGK Toán 8 tập 2 - Luyện tập
Bài 40, 41, 42, 43, 44, 45, 46 trang 31; bài 47, 48, 49 trang 32 SGK Toán 8 tập 2 - Luyện tập. Bài 40 trang 31 Năm nay, tuổi mẹ gấp 3 lần tuổi Phương. Phương tính rằng 13 năm nữa thì tuổi mẹ chỉ còn gấp 2 lần tuổi Phương thôi. Hỏi năm nay Phương bao nhiêu tuổi?
-

Bài 50, 51, 52, 53, 54, 55, 56 trang 33, 34 SGK Toán 8 tập 2 - Ôn tập chương 3
Bài 50, 51, 52 trang 33; bài 53, 54, 55, 56 trang 34 SGK Toán 8 tập 2 - Ôn tập chương 3. Bài 54 trang 34: Một canô xuôi dòng từ bến A đến bến B mất 4 giờ và ngược dòng từ bến B về bến A mất 5 giờ. Tính khoảng cách giữa hai bến A và B, biết rằng vận tốc của dòng nước là 2 km/h.

 Tải ngay
Tải ngay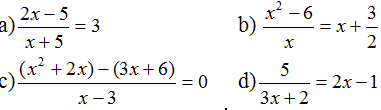
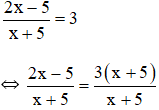
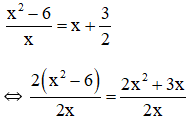
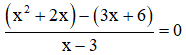
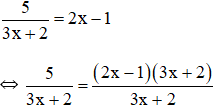
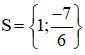
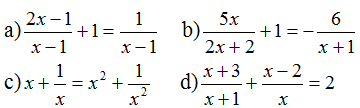
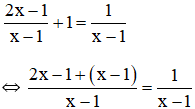
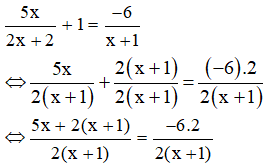
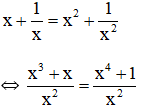
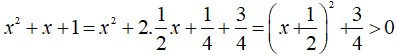 với mọi x).
với mọi x).