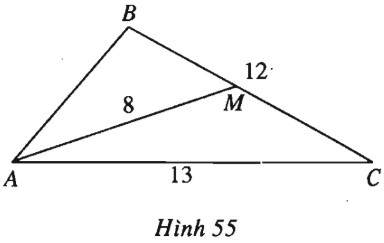
Bài 60 trang 48 SBT Hình học 10 Nâng caoGiải bài tập Bài 60 trang 48 SBT Hình học 10 Nâng cao Tam giác \(ABC\) có \(BC=12, CA=13\), trung tuyến \(AM=8.\) a) Tính diện tích tam giác \(ABC.\) b) Tính góc \(B.\) Giải (h.55).
a) Theo công thức Hê-rông ta có \({S_{AMC}} = \sqrt {\dfrac{{27}}{2}\left( {\dfrac{{27}}{2} - 13} \right)\left( {\dfrac{{27}}{2} - 6} \right)\left( {\dfrac{{27}}{2} - 8} \right)} = \dfrac{{9\sqrt {55} }}{4}.\) Suy ra \({S_{ABC}} = 2{S_{AMC}} = \dfrac{{9\sqrt {55} }}{2}\). b) Ta có \({b^2} + {c^2} = 2A{M^2} + \dfrac{{{a^2}}}{2}\). Suy ra \(A{B^2} = {c^2} = 2A{M^2} - {b^2} + \dfrac{{{a^2}}}{2}\) \(= 2.64 + 72 - 169 = 31 \Rightarrow c = \sqrt {31} \). Từ đó ta có \(\cos B = \dfrac{{31 + 144 - 169}}{{24\sqrt {31} }} \) \(= \dfrac{1}{{4\sqrt {31} }} \approx 0,045 \Rightarrow \widehat B \approx {87^0}25'.\) Sachbaitap.com
Xem thêm tại đây:
Bài 3. Hệ thức lượng trong tam giác.
|

 Tải ngay
Tải ngay