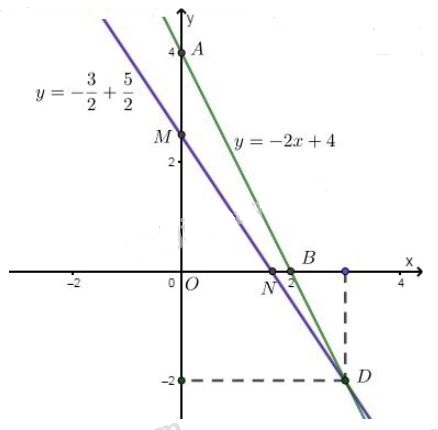
Bài 7, 8, 9, 10, 11 trang 12 SGK Toán 9 tập 2 - Luyện tập

Bài 7 trang 12 SGK Toán lớp 9 tập 2

Câu hỏi:

Cho hai phương trình \(2x + y = 4\) và \(3x + 2y = 5\).

a) Tìm nghiệm tổng quát của mỗi phương trình trên.

b) Vẽ các đường thẳng biểu diễn tập nghiệm của hai phương trình trong mỗi một hệ trục tọa độ, rồi xác định nghiệm chung của chúng.

Lời giải:

a) Ta có:

+) \(2x{\rm{ }} + {\rm{ }}y{\rm{ }} = {\rm{ }}4{\rm{ }} \Leftrightarrow {\rm{ }}y{\rm{ }} = {\rm{ }} - 2x{\rm{ }} + {\rm{ }}4{\rm{ }}\). 

Do đó phương trình có nghiệm dạng tổng quát là:

\(\left\{ \matrix{x \in R \hfill \cr y = - 2{\rm{x}} + 4 \hfill \cr} \right.\) 

+) \(3x + 2y = 5 \Leftrightarrow y =  - \dfrac{3}{2}x + \dfrac{5}{2}\).

Do đó phương trình có nghiệm tổng quát như sau: 

\(\left\{ \matrix{
x \in R\hfill \cr
y = - \dfrac{3}{2}x + \dfrac{5}{2} \hfill \cr} \right.\)

b) +) Vẽ \((d)\): \(y =-2x+ 4\)

Cho \(x = 0 \Rightarrow y = 4\)  được  \(A(0; 4)\).

Cho \(y = 0 \Rightarrow x = 2\)  được  \(B(2; 0)\).

Đường thẳng \((d)\) là đường thẳng đi qua hai điểm \(A,\ B\).

+) Vẽ \((d')\): \(y =-\dfrac{3}{2}x+\dfrac{ 5}{2}\)

Cho \(x = 0 \Rightarrow y = \dfrac{5 }{2}\),  ta được  \(M{\left(0;\dfrac{5}{2} \right)}\).

Cho \(y = 0 \Rightarrow x = \dfrac{5 }{3}\),  ta được  \(N {\left( \dfrac{5}{3};0 \right)}\).

Đường thẳng \((d')\) là đường thẳng đi qua hai điểm \(M,\ N\).

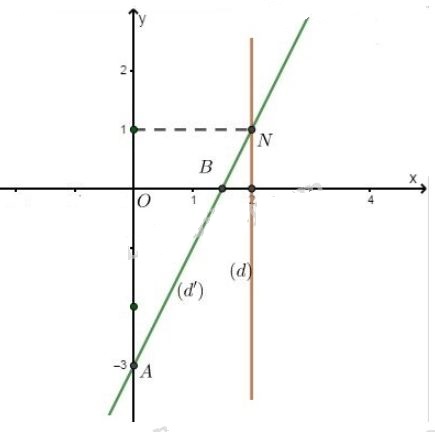
Hai đường thẳng cắt nhau tại \(D(3; -2)\).

Thay \(x = 3, y = -2\) vào từng phương trình ta được:

\(2 . 3 + (-2) = 4\) và \(3 . 3 + 2 . (-2) = 5\) (thỏa mãn)

Vậy \((3; -2)\) là nghiệm chung của các phương trình đã cho.

Bài 8 trang 12 SGK Toán lớp 9 tập 2

Câu hỏi:

Cho các hệ phương trình sau:

\(a)\left\{ \matrix{
x = 2 \hfill \cr 
2x - y = 3 \hfill \cr} \right.\)

\(b)\left\{ \matrix{
x + 3y = 2 \hfill \cr 
2y = 4 \hfill \cr} \right.\)

Trước hết, hãy đoán nhận số nghiệm của mỗi hệ phương trình trên (giải thích rõ lí do). Sau đó, tìm tập nghiệm của các hệ đã cho bằng cách vẽ hình.

Lời giải:

a) Ta có

\(\left\{ \matrix{
x = 2 \hfill \cr 
2x - y = 3 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = 2\ (d) \hfill \cr 
y = 2x - 3\ (d') \hfill \cr} \right.\)

Dự đoán: Hệ có nghiệm duy nhất vì một đồ thị là đường thẳng \((d):x = 2\) song song với trục tung, còn một đồ thị là đường thẳng \((d'):y = 2x - 3\) cắt hai trục tọa độ.

+) Vẽ \((d)\): \(x = 2\) là đường thẳng đi qua điểm có tọa độ \((2;0)\) và song song với trục \(Oy\).

+) Vẽ \((d' )\): \(y =2x- 3\)

Cho \(x = 0 \Rightarrow y = -3\) ta được \(A(0; -3)\).

Cho \(y = 0 \Rightarrow x = \dfrac{3}{2}\) ta được \(B{\left(\dfrac{3 }{2};0 \right)}\).

Đường thẳng (d') là đường thẳng đi qua hai điểm \(A,\ B\).

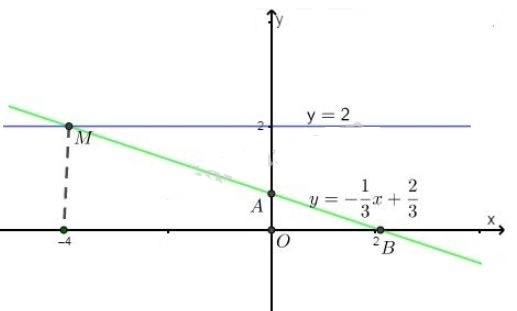
Ta thấy hai đường thẳng cắt nhau tại \(N(2; 1)\).

Thay \(x = 2, y = 1\) vào hệ phương trình 

\(\left\{ \begin{array}{l}x = 2\\2x - y = 3\end{array} \right.\) ta được 

\(\left\{ \begin{array}{l}2 = 2\\2.2 - 1 = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2 = 2\\3 = 3\end{array} \right.\)  (luôn đúng) 

Vậy hệ phương trình có nghiệm \((2; 1)\).

\(b)\left\{ \matrix{
x + 3y = 2 \hfill \cr
2y = 4 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
y = - \dfrac{1}{3}x + \dfrac{2}{3}\, (d)\hfill \cr
y = 2 \, (d') \hfill \cr}  \right.\)

Hệ có nghiệm duy nhất vì một đồ thị là đường thẳng \((d):y =  - \dfrac{1 }{3}x + \dfrac{2}{3}\) cắt hai trục tọa độ, còn một đồ thị là đường thẳng \((d'):y = 2\) song song với trục hoành.

+) Vẽ \(y=-\dfrac{1}{3}x+\dfrac{2}{3}\)

Cho \(x = 0 \Rightarrow y = \dfrac{2}{3}\) ta được \(A{\left(0;\dfrac{2}{3}\right)}\) .

Cho \(y = 0 \Rightarrow x = 2\) ta được \(B(2; 0)\).

Đồ thị hàm số \(y=-\dfrac{1}{3}x+\dfrac{2}{3}\) là đường thẳng đi qua hai điểm \(A,\ B\).

+) Vẽ  \(y = 2\) là đường thẳng đi qua điểm có tọa độ \((0;2)\) trên trục tung và song song với trục hoành (\(Ox\))

Bài 9 trang 12 SGK Toán lớp 9 tập 2

Câu hỏi:

Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:

a) \(\left\{\begin{matrix} x + y = 2 & & \\ 3x + 3y = 2 & & \end{matrix}\right.\);                 

b) \(\left\{\begin{matrix} 3x -2 y = 1 & & \\ -6x + 4y = 0 & & \end{matrix}\right.\)

Lời giải:

a) Ta có:

\(\left\{\begin{matrix} x + y = 2 & & \\ 3x + 3y = 2 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} y = -x + 2 & & \\ 3y = -3x+2 & & \end{matrix}\right. \)

\(\Leftrightarrow \left\{\begin{matrix} y = -x + 2 \, (d) & & \\ y = -x + \dfrac{2}{3} \, (d')& & \end{matrix}\right.\)

Suy ra \(a = -1,\ a' = -1\);  \(b = 2,\ b' = \dfrac{2}{3}\) nên \(a = a', b ≠ b'.\)

Do đó hai đường thẳng \((d)\) và \((d')\) song song nhau nên hệ đã cho vô nghiệm.

b) Ta có:

\(\left\{\begin{matrix} 3x -2 y = 1 & & \\ -6x + 4y = 0 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} 2y = 3x - 1 & & \\ 4y = 6x& & \end{matrix}\right. \)

\(\Leftrightarrow \left\{\begin{matrix} y = \dfrac{3}{2}x - \dfrac{1}{2} \,(d) & & \\ y = \dfrac{3}{2}x\, (d')& & \end{matrix}\right.\)

Ta có: \(a = \dfrac{3}{2}, a' = \dfrac{3}{2}\), \(b = -\dfrac{1}{2}, b' = 0\) nên \(a = a', b ≠b'\).

Do đó hai đường thẳng \((d)\) và \((d')\) song song với nhau nên hệ đã cho vô nghiệm. 

Bài 10 trang 12 SGK Toán lớp 9 tập 2

Câu hỏi:

Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:

a) \(\left\{\begin{matrix} 4x - 4y = 2 & & \\ -2x + 2y = -1 & & \end{matrix}\right.\)

b) \(\left\{\begin{matrix} \dfrac{1}{3}x - y = \dfrac{2}{3} & & \\ x -3y = 2 & & \end{matrix}\right.\)

Lời giải:

a) 

Ta có:

\(\left\{\begin{matrix} 4x - 4y = 2 & & \\ -2x + 2y = -1 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} 4y = 4x - 2 & & \\ 2y = 2x - 1 & & \end{matrix}\right. \)

\(\Leftrightarrow \left\{\begin{matrix} y = x - \dfrac{1}{2}\, (d)& & \\ y = x - \dfrac{1}{2} \, (d')& & \end{matrix}\right.\)

Suy ra \(a = a' = 1;\ b = b' = - \dfrac{1}{2}\).

Do đó hai đường thẳng \((d)\) và \((d')\)  trùng nhau nên hệ phương trình có vô số nghiệm.

b) 

Ta có:

\(\left\{\begin{matrix} \dfrac{1}{3}x - y = \dfrac{2}{3} & & \\ x -3y = 2 & & \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} y = \dfrac{1}{3}x - \dfrac{2}{3} & & \\ 3y = x - 2 & & \end{matrix}\right. \)

\(\Leftrightarrow \left\{\begin{matrix} y = \dfrac{1}{3}x - \dfrac{2}{3} \, (d)& & \\ y = \dfrac{1}{3}x - \dfrac{2}{3} \, (d')& & \end{matrix}\right.\)

Suy ra \(a = a' = \dfrac{1}{3}\), \(b = b' = -\dfrac{2}{3}\)

Do đó hai đường thẳng \((d)\) và \((d')\)  trùng nhau nên hệ phương trình có vô số nghiệm.

Bài 11 trang 12 SGK Toán lớp 9 tập 2

Câu hỏi:

Nếu tìm thấy hai nghiệm phân biệt của một hệ hai phương trình bậc nhất hai ẩn (nghĩa là hai nghiệm được biểu diễn bởi hai điểm phân biệt) thì ta có thể nói gì về số nghiệm của hệ phương trình đó ? Vì sao ?

Phương pháp: 

Sử dụng tính chất: Qua hai điểm phân biệt vẽ được một và chỉ một đường thẳng.

Lời giải:

Giả sử hệ hai phương trình bậc nhất hai ẩn: \(\left\{\begin{matrix} ax +by = c \ (d) & & \\ a'x + b'y = c' \ (d') & & \end{matrix}\right.\)

có hai nghiệm phân biệt. Khi đó \((d)\) và \((d')\) giao nhau tại hai điểm phân biệt \(A\) và \(B\).

Do đó \(A,\ B\) nằm trên đường thẳng \(d\).

Cũng có \(A,\ B\) cùng nằm trên đường thẳng \(d'\).

Vì qua hai điểm phân biệt ta luôn vẽ được một và chỉ một đường thẳng nên \(d\) và \(d'\) trùng nhau. Tức là hệ trên có vô số nghiệm.

Sachbaitap.com