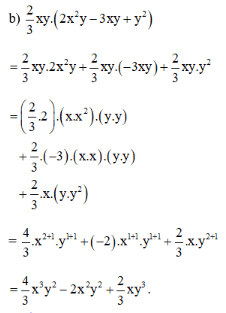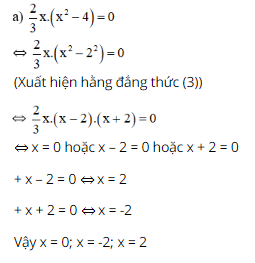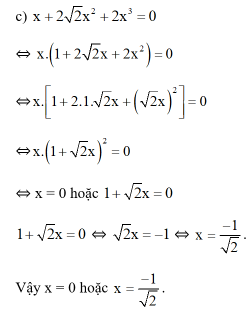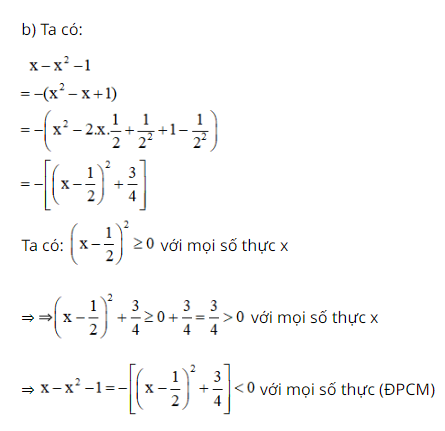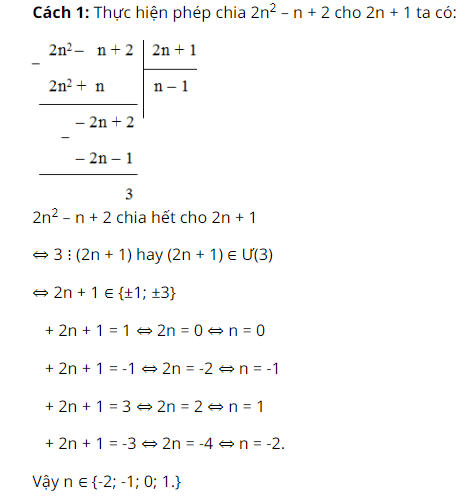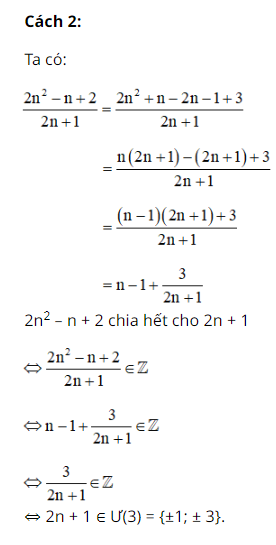Bài 75, 76, 77, 78, 79, 80, 81, 82, 83 trang 33 SGK Toán 8 tập 1 - Ôn tập chương 1

Bài 75 trang 33 SGK Toán lớp 8 tập 1

Câu hỏi:

Làm tính nhân:

a) \(5{x^2}.\left( {3{x^2} - 7x + 2} \right);\)                    

b) \({2 \over 3}xy.\left( {2{x^2}y - 3xy + {y^2}} \right)\).

Phương pháp:

Muốn nhân một đơn thức với một đa thức, ta lấy đơn thức nhân với từng hạng tử của đa thức rồi cộng các tích với nhau.

Lời giải:

a) 5x².(3x² – 7x + 2)

= 5x².3x² + 5x².(-7x) + 5x².2

= (5.3).(x².x²) + [5.(-7)].(x².x) + (5.2).x²

= 15x^{2 + 2} + (-35).x^{2 + 1} + 10.x²

= 15x⁴ – 35x³ + 10x²

Bài 76 trang 33 SGK Toán lớp 8 tập 1

Câu hỏi:

Làm tính nhân:  

\(\left( {2{x^2} - 3x} \right)\left( {5{x^2} - 2x + 1} \right)\)

\(\left( {x - 2y} \right)\left( {3xy + 5{y^2} + x} \right)\) .

Phương pháp:

Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.

Lời giải:

a) (2x² – 3x)(5x² – 2x + 1)

= 2x²(5x² – 2x + 1) + (-3x)(5x² – 2x + 1)

= 2x².5x² + 2x².(-2x) + 2x².1 + (–3x).5x² + (-3x).(-2x) + (-3x).1

= (2.5)(x².x²) + (2. (-2)).(x².x) + 2x² + [(-3).5].(x.x²) + [(-3).(-2).(x.x) + (-3x)

= 10x⁴ – 4x³ + 2x² – 15x³ + 6x² – 3x

= 10x⁴ – (4x³ + 15x³) + (2x² + 6x²) – 3x

= 10x⁴ – 19x³ + 8x² – 3x

b) (x – 2y)(3xy + 5y² + x)

= x.(3xy + 5y² + x) + (-2y).(3xy + 5y² + x)

= x.3xy + x.5y² + x.x + (-2y).3xy + (–2y).5y² + (–2y).x

= 3x²y + 5xy² + x² – 6xy² – 10y³ – 2xy

= 3x²y + (5xy² – 6xy²) + x² – 10y³ – 2xy

= 3x²y – xy² + x² – 10y³ – 2xy

Bài 77 trang 33 SGK Toán lớp 8 tập 1

Câu hỏi:

Tính nhanh giá trị của biểu thức:

a. \(M = {x^2} + 4{y^2} - 4xy\)  tại \(x = 18\) và \(y = 4\).

b. \(N = 8{x^3} - 12{x^2}y + 6x{y^2} - {y^3}\)  tại \(x = 6\) và \(y =- 8\).

Phương pháp:

a. Biến đổi để đưa \( M\) về dạng hằng đẳng thức. Sau đó thay giá trị của \(x;y\) vào để tính giá trị của biểu thức \(M\).

Sử dụng: \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)

b. Biến đổi để đưa \( N\) về dạng hằng đẳng thức. Sau đó thay giá trị của \(x;y\) vào để tính giá trị của biểu thức \(N\).

Sử dụng: \({\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\)

Lời giải:

a) M = x² + 4y² – 4xy

= x² – 2.x.2y + (2y)² (Hằng đẳng thức (2))

= (x – 2y)²

Thay x = 18, y = 4 ta được:

    M = (18 – 2.4)² = 10² = 100

b) N = 8x³ – 12x²y + 6xy² – y³

= (2x)³ – 3(2x)²y + 3.2xy² – y³ (Hằng đẳng thức (5))

= (2x – y)³

Thay x = 6, y = - 8 ta được:

    N = (2.6 – (-8))³ = 20³ = 8000

 Bài 78 trang 33 SGK Toán lớp 8 tập 1

Câu hỏi:

Rút gọn các biểu thức sau:

a.\(\left( {x + 2} \right)\left( {x - 2} \right) - \left( {x - 3} \right)\left( {x + 1} \right)\);

b. \({\left( {2x + 1} \right)^2} + {\left( {3x - 1} \right)^2} + 2\left( {2x + 1} \right)\left( {3x - 1} \right)\) .

Phương pháp:

a.

- Áp dụng quy tắc: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.

- Áp dụng hằng đẳng thức: 

\({A^2} - {B^2} = \left( {A + B} \right)\left( {A - B} \right)\)

Lời giải:

a) (x + 2)(x – 2) – (x – 3)(x + 1)

= x² – 2² – (x² + x – 3x – 3)

= x² – 4 – x² – x + 3x + 3

= 2x – 1

b) (2x + 1)² + (3x – 1)² + 2(2x + 1)(3x – 1)

= (2x + 1)² + 2.(2x + 1)(3x – 1) + (3x – 1)²

= [(2x + 1) + (3x – 1)]²

= (2x + 1 + 3x – 1)²

= (5x)²

= 25x²

Bài 79 trang 33 SGK Toán lớp 8 tập 1

Câu hỏi:

Phân tích các đa thức sau thành nhân tử:

\({x^2} - 4 + {\left( {x - 2} \right)^2}\) ;

\({x^3} - 2{x^2} + x - x{y^2}\) ;

\({x^3} - 4{x^2} - 12x + 27\). 

Phương pháp:

a.

Sử dụng các phương pháp phân tích đa thức thành nhân tử như đặt nhân tử chung, dùng hằng đẳng thức, nhóm hạng tử hoặc phối hợp các phương pháp.

Sử dụng: \({A^2} - {B^2} = \left( {A + B} \right)\left( {A - B} \right)\)

b.

Sử dụng các phương pháp phân tích đa thức thành nhân tử như đặt nhân tử chung, dùng hằng đẳng thức, nhóm hạng tử hoặc phối hợp các phương pháp.

Sử dụng: 

\(2)\,{\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)

\(3)\,{A^2} - {B^2} = \left( {A + B} \right)\left( {A - B} \right)\) 

c.

Sử dụng các phương pháp phân tích đa thức thành nhân tử như đặt nhân tử chung, dùng hằng đẳng thức, nhóm hạng tử hoặc phối hợp các phương pháp.

Sử dụng: \({A^3} + {B^3} = \left( {A + B} \right)({A^2} - AB + {B^2})\)

Lời giải:

a) Cách 1: x² – 4 + (x – 2)²

(Xuất hiện hằng đẳng thức (3))

= (x²– 2²) + (x – 2)²

= (x – 2)(x + 2) + (x – 2)²

(Có nhân tử chung x – 2)

= (x – 2)[(x + 2) + (x – 2)]

= (x – 2)(x + 2 + x – 2)

= (x – 2)(2x)

= 2x(x – 2)

Cách 2: x² – 4 + (x – 2)²

(Khai triển hằng đẳng thức (2))

= x² – 4 + (x² – 2.x.2 + 2²)

= x² – 4 + x² – 4x + 4

= 2x² – 4x

(Có nhân tử chung là 2x)

= 2x(x – 2)

 b) x³ – 2x² + x – xy²

(Có nhân tử chung x)

= x(x² – 2x + 1 – y²)

(Có x² – 2x + 1 là hằng đẳng thức).

= x[(x – 1)² – y²]

(Xuất hiện hằng đẳng thức (3))

= x(x – 1 + y)(x – 1 – y)

c) x³ – 4x² – 12x + 27

(Nhóm để xuất hiện nhân tử chung)

= (x³ + 27) – (4x² + 12x)

= (x³ + 3³) – (4x² + 12x)

(nhóm 1 là HĐT, nhóm 2 có 4x là nhân tử chung)

= (x + 3)(x² – 3x + 9) – 4x(x + 3)

= (x + 3)(x² – 3x + 9 – 4x)

= (x + 3)(x² – 7x + 9)

Bài 80 trang 33 SGK Toán lớp 8 tập 1

Câu hỏi:

Làm tính chia:  

\(\left( {6{x^3} - 7{x^2} - x + 2} \right):\left( {2x + 1} \right)\)

\(\left( {{x^4} - {x^3} + {x^2} + 3x} \right):\left( {{x^2} - 2x + 3} \right)\) ;

\(\left( {{x^2} - {y^2} + 6x + 9} \right):\left( {x + y + 3} \right)\) .

Phương pháp:

Áp dụng quy tắc chia đa thức một biến đã sắp xếp.

Lời giải:

Vậy (6x³ – 7x² – x + 2) : (2x + 1) = 3x² – 5x + 2

Cách 2: Phân tích 6x³ – 7x² – x + 2 thành (2x + 1).P(x) + R(x)

6x³ – 7x² – x + 2

= 6x³ + 3x² – 10x² – 5x + 4x + 2

(Tách -7x² = 3x² – 10x²; -x = -5x + 4x)

= 3x².(2x + 1) – 5x.(2x + 1) + 2.(2x + 1)

= (3x² – 5x + 2)(2x + 1)

Vậy (6x³ – 7x² – x + 2) : (2x + 1) = 3x² – 5x + 2

Giải thích cách tách:

Vì có 6x³ nên ta cần thêm 3x² để có thể phân tích thành 3x²(2x + 1). Do đó ta tách -7x² = 3x² – 10x².

Lại có -10x² nên ta cần thêm -5x để có thể phân tích thành -5x(2x + 1). Do đó ta tách –x = -5x + 4x.

 Có 4x, ta cần thêm 2 để có 2.(2x + 1) nên 2 không cần phải tách.

b. 

Vậy (x⁴ – x³ + x² + 3x) : (x² – 2x + 3) = x² + x

Cách 2: Phân tích x⁴ – x³ + x² + 3x thành nhân tử có chứa x² – 2x + 3 

x⁴ – x³ + x² + 3x

= x.(x³ – x² + x + 3)

= x.(x³ – 2x² + 3x + x² – 2x + 3)

= x.[x.(x² – 2x + 3) + (x² – 2x + 3)]

= x.(x + 1)(x² – 2x + 3)

Vậy (x⁴ – x³ + x² + 3x) : (x² – 2x + 3) = x(x + 1) = x² + x.

c) Phân tích số bị chia thành nhân tử, trong đó có nhân tử là số chia.

(x² – y² + 6x + 9) : (x + y + 3)

(Có x² + 6x + 9 là hằng đẳng thức)

= (x² + 6x + 9 – y²) : (x + y + 3)

= [(x² + 2.x.3 + 3²) – y²] : (x + y + 3)

= [(x + 3)² – y²] : (x + y + 3)

(Xuất hiện hằng đẳng thức (3))

= (x + 3 + y)(x + 3 – y) : (x + y + 3)

= x + 3 – y = x – y + 3

Bài 81 trang 33 SGK Toán lớp 8 tập 1

Câu hỏi:

Tìm \(x\), biết:

\(\dfrac{2}{3}x\left( {{x^2} - 4} \right) = 0\) ;

\({\left( {x + 2} \right)^2} - \left( {x - 2} \right)\left( {x + 2} \right) = 0\) ;

\(x + 2\sqrt 2 {x^2} + 2{x^3} = 0\) .

Phương pháp:

- Phân tích các đa thức ở vế trái thành nhân tử bằng phương pháp dùng hằng đẳng thức, đặt nhân tử chung.

- Áp dụng:

\(A.B = 0 \Rightarrow \left[ \begin{gathered}
A = 0 \hfill \\
B = 0 \hfill \\ 
\end{gathered} \right.\)

Lời giải:

b) (x + 2)² – (x – 2)(x + 2) = 0

(Có x + 2 là nhân tử chung)

⇔ (x + 2)[(x + 2) – (x – 2)] = 0

⇔ (x + 2)(x + 2 – x + 2) = 0

⇔ (x + 2).4 = 0

⇔ x + 2 = 0

⇔ x = - 2

Vậy x = -2

Bài 82 trang 33 SGK Toán lớp 8 tập 1

Câu hỏi:

Chứng minh:

\({x^2} - 2xy + {y^2} + 1 > 0\)  với mọi số thực \(x\) và \(y\);

\(x - {x^2} - 1 < 0\)  với mọi số thực \(x\).

Phương pháp:

Áp dụng:

- Hằng đẳng thức bình phương một hiệu.

- Tính chất: \({\left( {A - B} \right)^2} \geqslant 0\) với mọi số thực \(A,B\)

Lời giải:

a) Ta có:

x² – 2xy + y² + 1

= (x² – 2xy + y²) + 1

= (x – y)² + 1.

(x – y)² ≥ 0 với mọi x, y ∈ R

⇒ x² – 2xy + y² + 1 = (x – y)² + 1 ≥ 0 + 1 = 1 > 0 với mọi x, y ∈ R (ĐPCM).

Bài 83 trang 33 SGK Toán lớp 8 tập 1

Câu hỏi:

Tìm \(n \in\mathbb Z\)  để  \(2{n^2} - n + 2\)  chia hết cho \(2n +1\).

Phương pháp:

Thực hiện phép chia \((2{n^2} - n + 2) :(2n +1)\)  để tìm số dư, sau đó để phép chia là phép chia hết thì số dư phải chia hết cho \(2n+1\).

Lời giải:

⇔ 2n + 1 ∈ Ư(3) = {±1; ± 3}.

   + 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0

   + 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1

   + 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1

   + 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.

Vậy n ∈ {-2; -1; 0; 1.}

Chú ý: Đa thức A chia hết cho đa thức B khi phần dư của phép chia bằng 0.

Sachbaitap.com