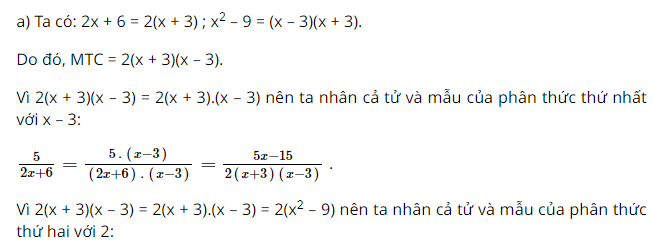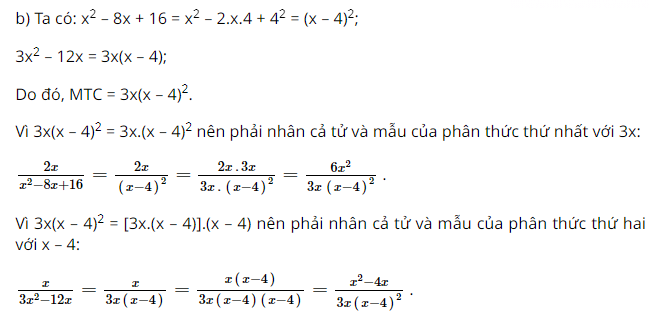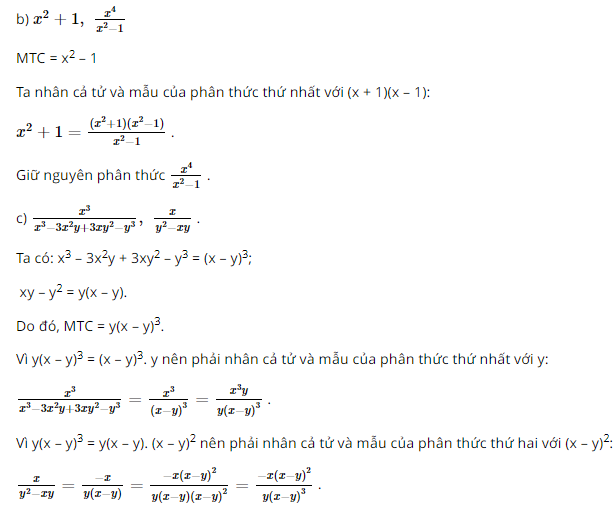Bài 14, 15, 16, 17, 18, 19, 20 trang 43, 44 SGK Toán 8 tập 1 - Quy đồng mẫu thức nhiều phân thức - luyện tậpBài 14, 15, 16, 17, 18, 19 trang 43, bài 20 trang 44 SGK Toán 8 tập 1 - Quy đồng mẫu thức nhiều phân thức - luyện tập. Bài 16. Quy đồng mẫu thức các phân thức sau (có thể áp dụng quy tắc đổi dấu đối với một phân thức để tìm mẫu thức chung thuận tiện hơn): Bài 14 trang 43 SGK Toán lớp 8 tập 1 Câu hỏi: Quy đồng mẫu thức các phân thức sau: a.\( \dfrac{5}{x^{5}y^{3}}, \dfrac{7}{12x^{3}y^{4}}\); b.\( \dfrac{4}{15x^{3}y^{5}}, \dfrac{11}{12x^{4}y^{2}}\) Phương pháp: Áp dụng quy tắc quy đồng mẫu thức: Muốn quy đồng mẫu thức nhiều phân thức ta có thể làm như sau: - Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung - Tìm nhân tử phụ của mỗi mẫu thức. - Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng. Lời giải:
Bài 15 trang 43 SGK Toán lớp 8 tập 1 Câu hỏi: Quy đồng mẫu các phân thức sau: a) \( \dfrac{5}{2x +6};\; \dfrac{3}{x^{2}-9}\); b) \( \dfrac{2x}{x^{2}-8x+16};\; \dfrac{x}{3x^{2}-12x}\) Phương pháp: Muốn quy đồng mẫu thức nhiều phân thức ta có thể làm như sau: - Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung. - Tìm nhân tử phụ của mỗi mẫu thức. - Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng. Lời giải:
Bài 16 trang 43 SGK Toán lớp 8 tập 1 Câu hỏi: Quy đồng mẫu thức các phân thức sau (có thể áp dụng quy tắc đổi dấu đối với một phân thức để tìm mẫu thức chung thuận tiện hơn): a.\( \dfrac{4x^{2}-3x+5}{x^{3}-1},\dfrac{1-2x}{x^{2}+x+1},-2\), b.\( \dfrac{10}{x+2},\dfrac{5}{2x-4},\dfrac{1}{6-3x}\) Phương pháp: - Áp dụng quy tắc đổi dấu. - Muốn quy đồng mẫu thức nhiều phân thức ta có thể làm như sau: + Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung. + Tìm nhân tử phụ của mỗi mẫu thức. + Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng. Lời giải:
Bài 17 trang 43 SGK Toán lớp 8 tập 1 Câu hỏi: Đố. Cho hai phân thức: \( \dfrac{5x^{2}}{x^{3}-6x^{2}},\dfrac{3x^{2}+18x}{x^{2}-36}\) Khi quy đồng mẫu thức, bạn Tuấn đã chọn \(MTC = {x^2}\left( {x - 6} \right)\left( {x + 6} \right)\), còn bạn Lan bảo rằng: "Quá đơn giản! \(MTC = x - 6\)". Đố em biết bạn nào chọn đúng? Phương pháp: Áp dụng qui tắc qui đồng mẫu thức các phân thức. Lời giải:
Khi đó MTC = x – 6. Nhận xét: Mẫu thức chung của cả hai bạn đưa ra đều đúng. Nhưng ta thấy MTC của bạn Lan ngắn gọn và dễ quy đồng hơn MTC của bạn Tuấn. Do đó, nếu phân thức chưa tối giản thì ta nên rút gọn từng phân thức trước rồi mới thực hiện quy đồng mẫu các phân thức. Bài 18 trang 43 SGK Toán lớp 8 tập 1 Câu hỏi: Quy đồng mẫu thức hai phân thức: \(\dfrac{{3x}}{{2x + 4}}\) và \(\dfrac{{x + 3}}{{{x^2} - 4}}\) \(\dfrac{{x + 5}}{{{x^2} + 4x + 4}}\) và \(\dfrac{x}{{3x + 6}}\) Phương pháp: Áp dụng quy tắc quy đồng mẫu thức: Muốn quy đồng mẫu thức nhiều phân thức ta có thể làm như sau: - Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung. - Tìm nhân tử phụ của mỗi mẫu thức. - Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng. Lời giải:
Bài 19 trang 43 SGK Toán lớp 8 tập 1 Câu hỏi: Quy đồng mẫu thức các phân thức sau: a. \(\dfrac{1}{{x + 2}},\dfrac{8}{{2x - {x^2}}}\) b. \({x^2} + 1,\dfrac{{{x^4}}}{{{x^2} - 1}}\) c. \(\dfrac{{{x^3}}}{{{x^3} - 3{x^2}y + 3x{y^2} - {y^3}}},\dfrac{x}{{{y^2} - xy}}\) Phương pháp: Áp dụng quy tắc quy đồng mẫu thức: Muốn quy đồng mẫu thức nhiều phân thức ta có thể làm như sau: - Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung. - Tìm nhân tử phụ của mỗi mẫu thức. - Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng. Lời giải:
Bài 20 trang 44 SGK Toán lớp 8 tập 1 Câu hỏi: Cho hai phân thức: \(\dfrac{1}{{{x^2} + 3x - 10}},\;\dfrac{x}{{{x^2} + 7x + 10}}\) Không dùng cách phân tích các mẫu thức thành nhân tử, hãy chứng tỏ rằng có thể quy đồng mẫu thức hai phân thức này với mẫu thức chung là \({x^3} + 5{x^2} - 4x - 20\) Phương pháp: Để chứng tỏ rằng có thể chọn đa thức \({x^3} + 5{x^2} - 4x - 20\) làm mẫu thức chung ta chỉ cần chứng tỏ rằng nó chia hết cho mẫu thức của mỗi phân thức đã cho. Lời giải: Thật vậy, ta có: x3 + 5x2 – 4x – 20 = x3 + 3x2 – 10x + 2x2 + 6x – 20 = x(x2 + 3x – 10) + 2(x2 + 3x – 10) = (x + 2)(x2 + 3x – 10) ⇒ x3 + 5x2 – 4x – 20 chia hết cho x2 + 3x – 10 x3 + 5x2 – 4x – 20 = x3 + 7x2 + 10x – 2x2 – 14x – 20 = x(x2 + 7x + 10) – 2.(x2 + 7x + 10) = (x – 2)(x2 + 7x + 10) ⇒ x3 + 5x2 – 4x – 20 chia hết cho x2 + 7x + 10 Do đó có thể chọn mẫu thức chung là x3 + 5x2 – 4x – 20. Sachbaitap.com
Xem thêm tại đây:
Chương II. Phân thức đại số
|
-

Bài 21, 22, 23, 24, 25, 26, 27 trang 46, 47, 48 SGK Toán 8 tập 1 - Phép cộng các phân thức đại số - luyện tập
Bài 21, 22, 23, 24 trang 46, bài 25, 26 trang 47, bài 27 trang 48 SGK Toán 8 tập 1 - Phép cộng các phân thức đại số - luyện tập. Bài 26 Một đội máy xúc trên công trường đường Hồ Chí Minh nhận nhiệm vụ xúc.
-

Bài 28, 29, 30, 31, 32 trang 49, 50 SGK Toán 8 tập 1 - Phép trừ các phân thức đại số
Bài 28 trang 49, bài 29, 30, 31, 32 trang 50 SGK Toán 8 tập 1 - Phép trừ các phân thức đại số. Bài 31. Chứng tỏ rằng mỗi hiệu sau đây bằng một phân thức có tử bằng 1:
-

Bài 33, 34, 35, 36, 37 trang 50, 51 SGK Toán 8 tập 1 - luyện tập
Bài 33, 34, 35 trang 50, bài 36, 37 trang 51 SGK Toán 8 tập 1 - luyện tập. Bài 37 Đố. Đố em tìm được một phân thức mà khi lấy phân thức đã cho trừ đi phân thức phải tìm thì được một phân thức bằng phân thức đối của phân thức đã cho.
-

Bài 38, 39, 40, 41 trang 52, 53 SGK Toán 8 tập 1 - Phép nhân các phân thức đại số
Bài 38, 39 trang 52, bài 40, 41 trang 53 SGK Toán 8 tập 1 - Phép nhân các phân thức đại số. Bài 41 Đố. Đố em điền được vào chỗ trống của phép nhân dưới đây những phân thức có mẫu thức bằng tử thức cộng với (1) ( dfrac{1}{x}.dfrac{x}{x+1}....=dfrac{1}{x+7})

 Tải ngay
Tải ngay