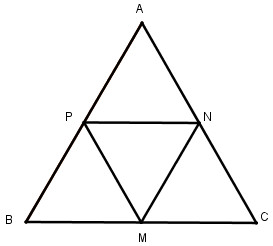
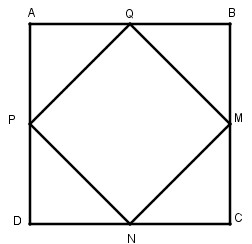
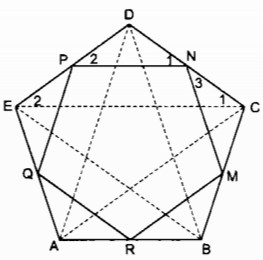
Câu 1.2 trang 156 Sách bài tập (SBT) Toán 8 tập 1Chứng minh MNP là tam giác đều. a. Cho tam giác đều ABC. Gọi M,N,P tương ứng là trung điểm của các cạnh BC, CA, AB. Chứng minh MNP là tam giác đều. b. Cho hình vuông ABCD. Gọi M, N, P, Q tương ứng là trung điểm của các cạnh BC, CD, DA, AB. Chứng minh MNPQ là hình vuông (tứ giác đều) c. Cho ngũ giác đều ABCDE. Gọi M, N, P, Q,, R tương ứng là trung điểm của các cạnh BC, CD, DE, EA, AB. Chứng minh MNPQR là ngũ giác đều. Giải:
a. Ta có: M là trung điểm của BC N là trung điểm của AC nên MN là đường trung bình của ∆ ABC ⇒ MN = \({1 \over 2}\)AB Ta có: P là trung điểm của AB nên MP là đường trung bình của ∆ ABC ⇒ MP = \({1 \over 2}\)AC NP là đường trung bình của ∆ ABC ⇒ NP = \({1 \over 2}\)BC mà AB = BC = AC (gt) ⇒ MN = MP = NP. Vậy ∆ MNP đều b.
Xét ∆ APQ và ∆ BQM: AQ = BQ (gt) \(\widehat A = \widehat B = {90^0}\) AP = BM (gt) Do đó: ∆ APQ = ∆ BQM (c.g.c) ⇒ PQ = QM (1) Xét ∆ BQM và ∆ CMN: BM = CM (gt) \(\widehat B = \widehat C = {90^0}\) BQ = CN (gt) Do đó: ∆ BQM = ∆ CMN (c.g.c) ⇒ QM = MN (2) Xét ∆ CMN và ∆ DNP: CN = DN (gt) \(\widehat C = \widehat D = {90^0}\) CM = DP (gt) Do đó: ∆ CMN = ∆ DNP (c.g.c) ⇒ MN = NP (3) Từ (1), (2) và (3) suy ra: MN = NP = PQ = QM nên tứ giác MNPQ là hình thoi Vì AP = AQ nên ∆ APQ vuông cân tại A BQ = BM nên ∆ BMQ vuông cân tại B \( \Rightarrow \widehat {AQP} = \widehat {BQM} = {45^0}\) \(\widehat {AQP} + \widehat {PQM} + \widehat {BQM} = {180^0}\) (kề bù) \( \Rightarrow \widehat {PQM} = {180^0} - \left( {\widehat {AQP} + \widehat {BQM}} \right)\) \(= {180^0} - \left( {{{45}^0} + {{45}^0}} \right) = {90^0}\) Vậy tứ giác MNPQ là hình vuông. c.
Xét ∆ ABC và ∆ BCD: AB = BC (gt) \(\widehat B = \widehat C\) (gt) BC = CD (gt) Do đó: ∆ ABC = ∆ BCD (c.g.c) ⇒ AC = BD (1) Xét ∆ BCD và ∆ CDE: BC = CD (gt) \(\widehat C = \widehat D\) (gt) CD = DE (gt) Do đó: ∆ BCD = ∆ CDE (c.g.c) ⇒ BD = CE (2) Xét ∆ CDE và ∆ DEA: CD = DE (gt) \(\widehat D = \widehat E\) (gt) DE = EA (gt) Do đó: ∆ CDE = ∆ DEA (c.g.c) ⇒ CE = DA (3) Xét ∆ DEA và ∆ EAB: DE = EA (gt) \(\widehat E = \widehat A\) (gt) EA = AB (gt) Do đó: ∆ DEA = ∆ EAB (c.g.c) ⇒ DA = EB (4) Từ (1), (2), (3), (4) suy ra: AC = BD = CE = DA = EB Trong ∆ ABC ta có RM là đường trung bình ⇒ RM = \({1 \over 2}\)AC (tính chất đường trung bình của tam giác) Mặt khác, ta có: Trong ∆ BCD ta có MN là đường trung bình ⇒ MN = \({1 \over 2}\)BD (tính chất đường trung bình của tam giác) Trong ∆ CDE ta có NP là đường trung bình ⇒ NP = \({1 \over 2}\)CE (tính chất đường trung bình của tam giác) Trong ∆ 9DEA ta có PQ là đường trung bình ⇒ PQ = \{1 \over 2}\)DA (tính chất đường trung bình của tam giác) Trong ∆ EAB ta có QR là đường trung bình ⇒ QR = \({1 \over 2}\)EB (tính chất đường trung bình của tam giác) Suy ra: MN = NP = PQ = QR = RM Ta có: \(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E = {{\left( {5 - 2} \right){{.180}^0}} \over 5} = {108^0}\) ∆ DPN cân tại D \( \Rightarrow \widehat {DPN} = \widehat {DNP} = {{{{180}^0} - \widehat D} \over 2} = {{{{180}^0} - {{108}^0}} \over 2} = {36^0}\) ∆ CNM cân tại C \( \Rightarrow \widehat {CNM} = \widehat {CMN} = {{{{180}^0} - \widehat C} \over 2} = {{{{180}^0} - {{108}^0}} \over 2} = {36^0}\) \(\widehat {ADN} + \widehat {PNM} + \widehat {CNM} = {180^0}\) \( \Rightarrow \widehat {PNM} = {180^0} - \left( {\widehat {ADN} + \widehat {CNM}} \right)\) \(= {180^0} - \left( {{{36}^0} + {{36}^0}} \right) = {108^0}\) ∆ BMR cân tại B \(\eqalign{ & \Rightarrow \widehat {BMR} = \widehat {BRM} = {{180^\circ - \widehat B} \over 2} = {{180^\circ - 108^\circ } \over 2} = 36^\circ \cr & \widehat {CMN} + \widehat {NMR} + \widehat {BMR} = 180^\circ \cr & \Rightarrow \widehat {NMR} \cr &= 180^\circ - \left( {\widehat {CMN} + \widehat {BMR}} \right) \cr & = 180^\circ - \left( {36^\circ + 36^\circ } \right) = 108^\circ \cr} \) ∆ ARQ cân tại A \(\eqalign{ & \Rightarrow \widehat {ARQ} = \widehat {AQR} = {{180^\circ - \widehat A} \over 2} = {{180^\circ - 108^\circ } \over 2} = 36^\circ \cr & \widehat {BRM} + \widehat {MRQ} + \widehat {ARQ} = 180^\circ \cr & \Rightarrow \widehat {MRQ} = 180^\circ - \left( {\widehat {BRM} + \widehat {ARQ}} \right) \cr & = 180^\circ - \left( {36^\circ + 36^\circ } \right) = 108^\circ \cr} \) ∆ QEP cân tại E \(\eqalign{ & \Rightarrow \widehat {EQP} = \widehat {EPQ} = {{180^\circ - \widehat E} \over 2} = {{180^\circ - 108^\circ } \over 2} = 36^\circ \cr & \widehat {AQR} + \widehat {RQP} + \widehat {EQP} = 180^\circ \cr & \Rightarrow \widehat {RQP} = 180^\circ - \left( {\widehat {AQR} + \widehat {EQP}} \right) \cr & = 180^\circ - \left( {36^\circ + 36^\circ } \right) = 108^\circ \cr & \widehat {EPQ} + \widehat {QPN} + \widehat {DPN} = 180^\circ \cr & \Rightarrow \widehat {QPN} = 180^\circ - \left( {\widehat {EPQ} + \widehat {DPN}} \right) \cr & = 180^\circ - \left( {36^\circ + 36^\circ } \right) = 108^\circ \cr} \) Suy ra : \(\widehat {PNM} = \widehat {NMR} = \widehat {MRQ} = \widehat {RQP} = \widehat {QPN}\) Vậy MNPQR là ngũ giác đều. Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 1. Đa giác – Đa giác đều
|
-
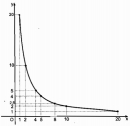
Câu 13 trang 157 Sách bài tập (SBT) Toán 8 tập 1-
Cho hình chữ nhật có diện tích là 20 ( đơn vị diện tích) và hai kích thước là x và y (đơn vị dài)
-
Câu 14 trang 157 Sách bài tập (SBT) Toán 8 tập 1
Diện tích của hình chữ nhật tăng bao nhiêu phần trăm nếu mỗi cạnh tăng 10% ?

 Tải ngay
Tải ngay