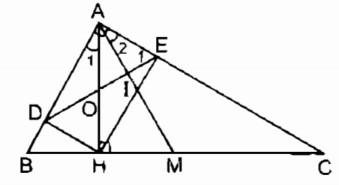
Câu 123 trang 95 Sách bài tập (SBT) Toán 8 tập 1Cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AM. Cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AM. a. Chứng minh rằng \(\widehat {HAB} = \widehat {MAC}\) b. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Chứng minh rằng AM vuông góc với DE. Giải:
a. AH ⊥ BC (gt) \( \Rightarrow \widehat {HAB} + \widehat B = {90^0}\) \(\widehat B + \widehat C = {90^0}\) (vì ∆ ABC có\(\widehat A = {90^0}\)) Suy ra: \(\widehat {HAB} = \widehat C\) (1) ∆ ABC vuông tại A có AM là trung tuyến thuộc cạnh huyền BC ⇒ AM = MC = \({1 \over 2}\) BC (tính chất tam giác vuông) ⇒ ∆ MAC cân tại M \( \Rightarrow \widehat {MAC} = \widehat C\) (tính chất tam giác vuông) (2) Từ (1) và (2) suy ra: \(\widehat {HAB} = \widehat {MAC}\) b. xét tứ giác ADHE có: \(\widehat A = {90^0}\) (gt) \(\widehat {ADH} = {90^0}\) (vì HD ⊥ AB) \(\widehat {AEH} = {90^0}\) (vì HE ⊥ AC) Suy ra: Tứ giác ADHE là hình chữ nhật (vì có ba góc vuông) ⇒ ∆ ADH = ∆ EHD (c.c.c) \( \Rightarrow {\widehat A_1} = \widehat {HED}\) \(\widehat {HED} + {\widehat E_1} = \widehat {HEA} = {90^0}\) Suy ra: \({\widehat E_1} + {\widehat A_1} = {90^0}\) \({\widehat A_1} = {\widehat A_2}\) (chứng minh trên) \( \Rightarrow {\widehat E_1} + {\widehat A_2} = {90^0}\) Gọi I là giao điểm của AM và DE Trong ∆ AIE ta có: \(\widehat {AIE} = {180^0} - \left( {{{\widehat E}_1} + {{\widehat A}_1}} \right) = {180^0} - {90^0} = {90^0}\) \(\Rightarrow \)AM ⊥ DE. Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 9. Hình chữ nhật
|
-

Câu 9.1 trang 95 Sách bài tập (SBT) Toán 8 tập 1
Một hình chữ nhật có hai cạnh kề bằng nhau 4cm và 6cm. Độ dài đường chéo của hình chữ nhật đó bằng bao nhiêu xentimét ?
-
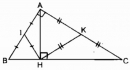
Câu 9.2 trang 95 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là trung điểm của AB, AC. Tính số đo góc IHK.
-
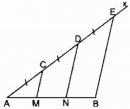
Câu 124 trang 95 Sách bài tập (SBT) Toán 8 tập 1
Chứng minh rằng đoạn thẳng AB bị chia ra ba phần bằng nhau.
-
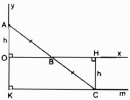
Câu 125 trang 95 Sách bài tập (SBT) Toán 8 tập 1
Cho góc vuông xOy, điểm A trên tia Oy. Điểm B di chuyển trên tia Ox. Gọi C là điểm đối xứng với A qua B. Điểm C di chuyển trên đường nào ?

 Tải ngay
Tải ngay